Menu Close

y-cosy-siny-1-cosx-sinx-1-

Tinku Tara 0 Comments
Pin




Question Number 121827 by bounhome last updated on 12/Nov/20
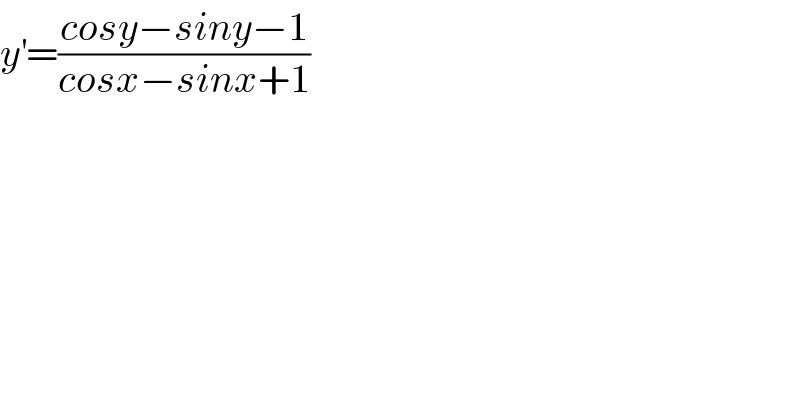
y^′ =((cosy−siny−1)/(cosx−sinx+1))
$${y}^{'} =\frac{{cosy}−{siny}−\mathrm{1}}{{cosx}−{sinx}+\mathrm{1}}\: \\ $$
Answered by TANMAY PANACEA last updated on 12/Nov/20
(dy/dx)=((cosy−siny−1)/(cosx−sinx+1)) (dy/(cosy−siny−1))=(dx/(cosx−sinx+1)) b=tan(y/2) a=tan(x/2) db=sec^2 ((y/2))×(1/2)×dy→dy=((2db)/(1+b^2 )) & dx=((2da)/(1+a^2 )) ∫((2db)/((((1−b^2 )/(1+b^2 ))−((2b)/(1+b^2 ))−1)×(1+b^2 )))=∫((2da)/((((1−a^2 )/(1+a^2 ))−((2a)/(1+a^2 ))+1)×(1+a^2 ))) ∫((2db)/(1−b^2 −2b−1−b^2 ))=∫((2da)/(1−a^2 −2a+1+a^2 )) ∫(db/(−2b^2 −2b))=∫(da/(2−2a)) ∫(db/(b^2 +b))=∫(da/(a−1)) ∫((b+1−b)/(b(b+1)))db=∫(da/(a−1)) ∫(db/b)−∫(db/(b+1))=∫(da/(a−1)) lnb−ln(b+1)=ln(a−1)+lnC ln((b/(b+1)))=ln{C×(a−1)} (b/(b+1))=C(a−1) ((tan(y/2))/(1+tan(y/2)))=C(tan(x/2)−1)
$$\frac{{dy}}{{dx}}=\frac{{cosy}−{siny}−\mathrm{1}}{{cosx}−{sinx}+\mathrm{1}} \\ $$$$\frac{{dy}}{{cosy}−{siny}−\mathrm{1}}=\frac{{dx}}{{cosx}−{sinx}+\mathrm{1}} \\ $$$${b}={tan}\frac{{y}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:{a}={tan}\frac{{x}}{\mathrm{2}} \\ $$$${db}={sec}^{\mathrm{2}} \left(\frac{{y}}{\mathrm{2}}\right)×\frac{\mathrm{1}}{\mathrm{2}}×{dy}\rightarrow{dy}=\frac{\mathrm{2}{db}}{\mathrm{1}+{b}^{\mathrm{2}} }\:\&\:\:{dx}=\frac{\mathrm{2}{da}}{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$$\int\frac{\mathrm{2}{db}}{\left(\frac{\mathrm{1}−{b}^{\mathrm{2}} }{\mathrm{1}+{b}^{\mathrm{2}} }−\frac{\mathrm{2}{b}}{\mathrm{1}+{b}^{\mathrm{2}} }−\mathrm{1}\right)×\left(\mathrm{1}+{b}^{\mathrm{2}} \right)}=\int\frac{\mathrm{2}{da}}{\left(\frac{\mathrm{1}−{a}^{\mathrm{2}} }{\mathrm{1}+{a}^{\mathrm{2}} }−\frac{\mathrm{2}{a}}{\mathrm{1}+{a}^{\mathrm{2}} }+\mathrm{1}\right)×\left(\mathrm{1}+{a}^{\mathrm{2}} \right)} \\ $$$$\int\frac{\mathrm{2}{db}}{\mathrm{1}−{b}^{\mathrm{2}} −\mathrm{2}{b}−\mathrm{1}−{b}^{\mathrm{2}} }=\int\frac{\mathrm{2}{da}}{\mathrm{1}−{a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$$\int\frac{{db}}{−\mathrm{2}{b}^{\mathrm{2}} −\mathrm{2}{b}}=\int\frac{{da}}{\mathrm{2}−\mathrm{2}{a}} \\ $$$$\int\frac{{db}}{{b}^{\mathrm{2}} +{b}}=\int\frac{{da}}{{a}−\mathrm{1}} \\ $$$$\int\frac{{b}+\mathrm{1}−{b}}{{b}\left({b}+\mathrm{1}\right)}{db}=\int\frac{{da}}{{a}−\mathrm{1}} \\ $$$$\int\frac{{db}}{{b}}−\int\frac{{db}}{{b}+\mathrm{1}}=\int\frac{{da}}{{a}−\mathrm{1}} \\ $$$${lnb}−{ln}\left({b}+\mathrm{1}\right)={ln}\left({a}−\mathrm{1}\right)+{lnC} \\ $$$${ln}\left(\frac{{b}}{{b}+\mathrm{1}}\right)={ln}\left\{{C}×\left({a}−\mathrm{1}\right)\right\} \\ $$$$\frac{{b}}{{b}+\mathrm{1}}={C}\left({a}−\mathrm{1}\right) \\ $$$$\frac{{tan}\frac{{y}}{\mathrm{2}}}{\mathrm{1}+{tan}\frac{{y}}{\mathrm{2}}}={C}\left({tan}\frac{{x}}{\mathrm{2}}−\mathrm{1}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *