Menu Close

y-dx-x-ln-x-ln-y-1-dy-0-where-y-1-0-

Tinku Tara 0 Comments
Pin




Question Number 125958 by bramlexs22 last updated on 15/Dec/20
y dx +x(ln x −ln y−1)dy=0 where y(1)=0
$$\:\:\:\:{y}\:{dx}\:+{x}\left(\mathrm{ln}\:{x}\:−\mathrm{ln}\:{y}−\mathrm{1}\right){dy}=\mathrm{0} \\ $$$$\:\:\:\:{where}\:{y}\left(\mathrm{1}\right)=\mathrm{0} \\ $$
Answered by Olaf last updated on 16/Dec/20
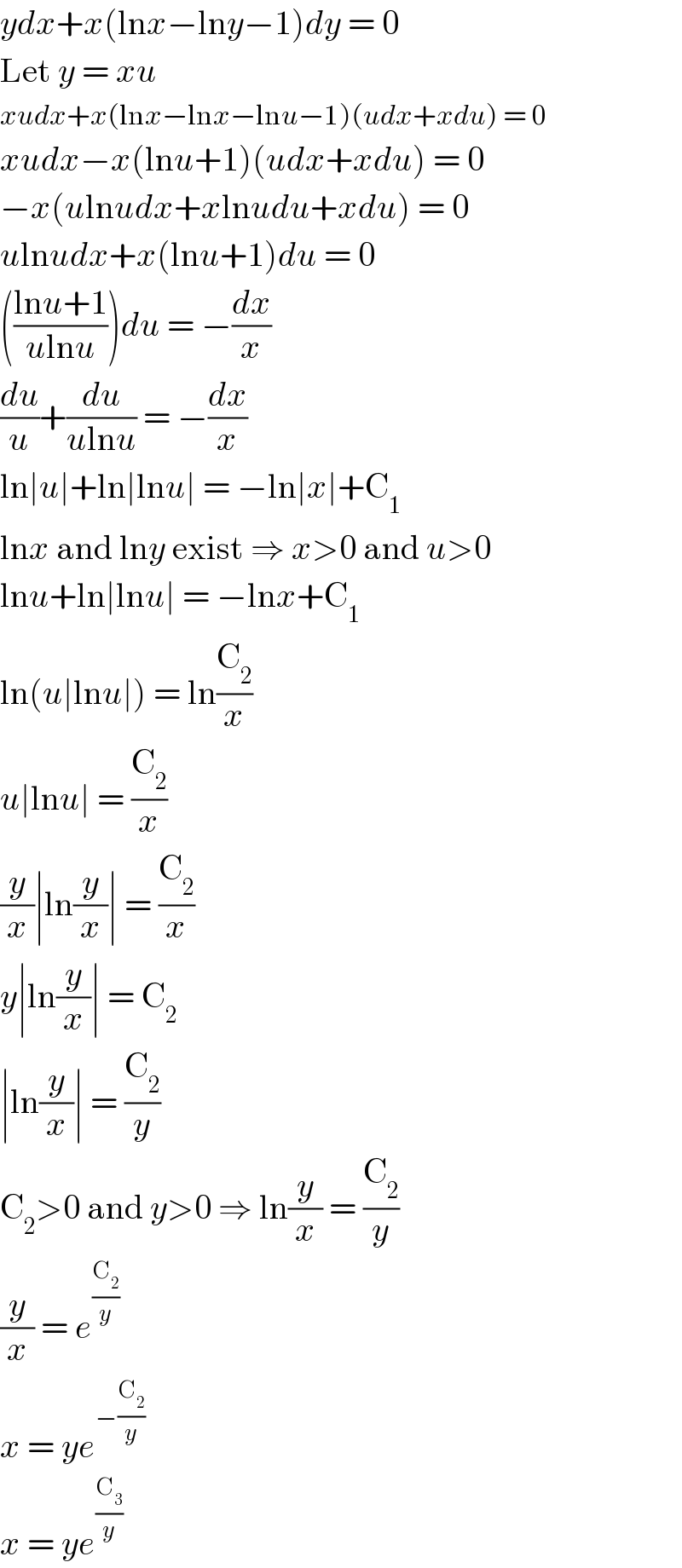
ydx+x(lnx−lny−1)dy = 0 Let y = xu xudx+x(lnx−lnx−lnu−1)(udx+xdu) = 0 xudx−x(lnu+1)(udx+xdu) = 0 −x(ulnudx+xlnudu+xdu) = 0 ulnudx+x(lnu+1)du = 0 (((lnu+1)/(ulnu)))du = −(dx/x) (du/u)+(du/(ulnu)) = −(dx/x) ln∣u∣+ln∣lnu∣ = −ln∣x∣+C_1 lnx and lny exist ⇒ x>0 and u>0 lnu+ln∣lnu∣ = −lnx+C_1 ln(u∣lnu∣) = ln(C_2 /x) u∣lnu∣ = (C_2 /x) (y/x)∣ln(y/x)∣ = (C_2 /x) y∣ln(y/x)∣ = C_2 ∣ln(y/x)∣ = (C_2 /y) C_2 >0 and y>0 ⇒ ln(y/x) = (C_2 /y) (y/x) = e^(C_2 /y) x = ye^(−(C_2 /y)) x = ye^(C_3 /y)
$${ydx}+{x}\left(\mathrm{ln}{x}−\mathrm{ln}{y}−\mathrm{1}\right){dy}\:=\:\mathrm{0} \\ $$$$\mathrm{Let}\:{y}\:=\:{xu} \\ $$$${xudx}+{x}\left(\mathrm{ln}{x}−\mathrm{ln}{x}−\mathrm{ln}{u}−\mathrm{1}\right)\left({udx}+{xdu}\right)\:=\:\mathrm{0} \\ $$$${xudx}−{x}\left(\mathrm{ln}{u}+\mathrm{1}\right)\left({udx}+{xdu}\right)\:=\:\mathrm{0} \\ $$$$−{x}\left({u}\mathrm{ln}{udx}+{x}\mathrm{ln}{udu}+{xdu}\right)\:=\:\mathrm{0} \\ $$$${u}\mathrm{ln}{udx}+{x}\left(\mathrm{ln}{u}+\mathrm{1}\right){du}\:=\:\mathrm{0} \\ $$$$\left(\frac{\mathrm{ln}{u}+\mathrm{1}}{{u}\mathrm{ln}{u}}\right){du}\:=\:−\frac{{dx}}{{x}} \\ $$$$\frac{{du}}{{u}}+\frac{{du}}{{u}\mathrm{ln}{u}}\:=\:−\frac{{dx}}{{x}} \\ $$$$\mathrm{ln}\mid{u}\mid+\mathrm{ln}\mid\mathrm{ln}{u}\mid\:=\:−\mathrm{ln}\mid{x}\mid+\mathrm{C}_{\mathrm{1}} \\ $$$$\mathrm{ln}{x}\:\mathrm{and}\:\mathrm{ln}{y}\:\mathrm{exist}\:\Rightarrow\:{x}>\mathrm{0}\:\mathrm{and}\:{u}>\mathrm{0} \\ $$$$\mathrm{ln}{u}+\mathrm{ln}\mid\mathrm{ln}{u}\mid\:=\:−\mathrm{ln}{x}+\mathrm{C}_{\mathrm{1}} \\ $$$$\mathrm{ln}\left({u}\mid\mathrm{ln}{u}\mid\right)\:=\:\mathrm{ln}\frac{\mathrm{C}_{\mathrm{2}} }{{x}} \\ $$$${u}\mid\mathrm{ln}{u}\mid\:=\:\frac{\mathrm{C}_{\mathrm{2}} }{{x}} \\ $$$$\frac{{y}}{{x}}\mid\mathrm{ln}\frac{{y}}{{x}}\mid\:=\:\frac{\mathrm{C}_{\mathrm{2}} }{{x}} \\ $$$${y}\mid\mathrm{ln}\frac{{y}}{{x}}\mid\:=\:\mathrm{C}_{\mathrm{2}} \\ $$$$\mid\mathrm{ln}\frac{{y}}{{x}}\mid\:=\:\frac{\mathrm{C}_{\mathrm{2}} }{{y}} \\ $$$$\mathrm{C}_{\mathrm{2}} >\mathrm{0}\:\mathrm{and}\:{y}>\mathrm{0}\:\Rightarrow\:\mathrm{ln}\frac{{y}}{{x}}\:=\:\frac{\mathrm{C}_{\mathrm{2}} }{{y}} \\ $$$$\frac{{y}}{{x}}\:=\:{e}^{\frac{\mathrm{C}_{\mathrm{2}} }{{y}}} \\ $$$${x}\:=\:{ye}^{−\frac{\mathrm{C}_{\mathrm{2}} }{{y}}} \\ $$$${x}\:=\:{ye}^{\frac{\mathrm{C}_{\mathrm{3}} }{{y}}} \\ $$
Answered by liberty last updated on 17/Dec/20
y dx = (1+ln y−ln x)x dy (dy/dx) = (y/(x(1+ln y−ln x))) ; let y = zx ⇔ z+x(dz/dx) = ((zx)/(x(1+ln zx−ln x))) z+x (dz/dx) = (z/(1+ln z)) ; x (dz/dx) = ((−zln z)/(1+ln z)) ⇔(((1+ln z)dz)/(zln z)) = −(dx/x) ∫ (dz/(zln z))+∫(dz/z) = −∫(dx/x) ⇔ln z+ln (ln z)+ln x = C ⇔ ln (zxln z)= C ⇒zxln z = C_1 ((y/x))xln ((y/x))=C_1 ⇒yln ((y/x))=C_1 ⇔(y/x) = e^(C_1 /y) ; y(1)=0 ⇒not correct
$${y}\:{dx}\:=\:\left(\mathrm{1}+\mathrm{ln}\:{y}−\mathrm{ln}\:{x}\right){x}\:{dy} \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{{y}}{{x}\left(\mathrm{1}+\mathrm{ln}\:{y}−\mathrm{ln}\:{x}\right)}\:;\:{let}\:{y}\:=\:{zx}\: \\ $$$$\Leftrightarrow\:{z}+{x}\frac{{dz}}{{dx}}\:=\:\frac{{zx}}{{x}\left(\mathrm{1}+\mathrm{ln}\:{zx}−\mathrm{ln}\:{x}\right)} \\ $$$${z}+{x}\:\frac{{dz}}{{dx}}\:=\:\frac{{z}}{\mathrm{1}+\mathrm{ln}\:{z}}\:;\:{x}\:\frac{{dz}}{{dx}}\:=\:\frac{−{z}\mathrm{ln}\:{z}}{\mathrm{1}+\mathrm{ln}\:{z}} \\ $$$$\Leftrightarrow\frac{\left(\mathrm{1}+\mathrm{ln}\:{z}\right){dz}}{{z}\mathrm{ln}\:{z}}\:=\:−\frac{{dx}}{{x}} \\ $$$$\int\:\frac{{dz}}{{z}\mathrm{ln}\:{z}}+\int\frac{{dz}}{{z}}\:=\:−\int\frac{{dx}}{{x}} \\ $$$$\Leftrightarrow\mathrm{ln}\:{z}+\mathrm{ln}\:\left(\mathrm{ln}\:{z}\right)+\mathrm{ln}\:{x}\:=\:{C} \\ $$$$\Leftrightarrow\:\mathrm{ln}\:\left({zx}\mathrm{ln}\:{z}\right)=\:{C}\:\Rightarrow{zx}\mathrm{ln}\:{z}\:=\:{C}_{\mathrm{1}} \\ $$$$\left(\frac{{y}}{{x}}\right){x}\mathrm{ln}\:\left(\frac{{y}}{{x}}\right)={C}_{\mathrm{1}} \:\Rightarrow{y}\mathrm{ln}\:\left(\frac{{y}}{{x}}\right)={C}_{\mathrm{1}} \\ $$$$\Leftrightarrow\frac{{y}}{{x}}\:=\:{e}^{\frac{{C}_{\mathrm{1}} }{{y}}} \:;\:{y}\left(\mathrm{1}\right)=\mathrm{0}\:\Rightarrow{not}\:{correct} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *