Question Number 123342 by bemath last updated on 25/Nov/20
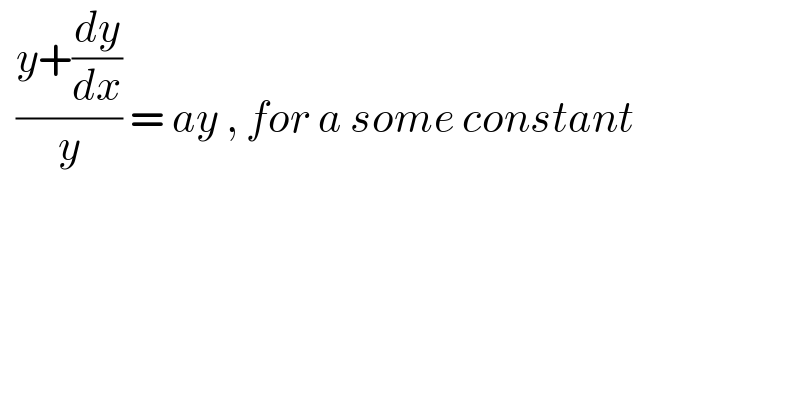
$$\:\:\frac{{y}+\frac{{dy}}{{dx}}}{{y}}\:=\:{ay}\:,\:{for}\:{a}\:{some}\:{constant} \\ $$
Answered by liberty last updated on 25/Nov/20
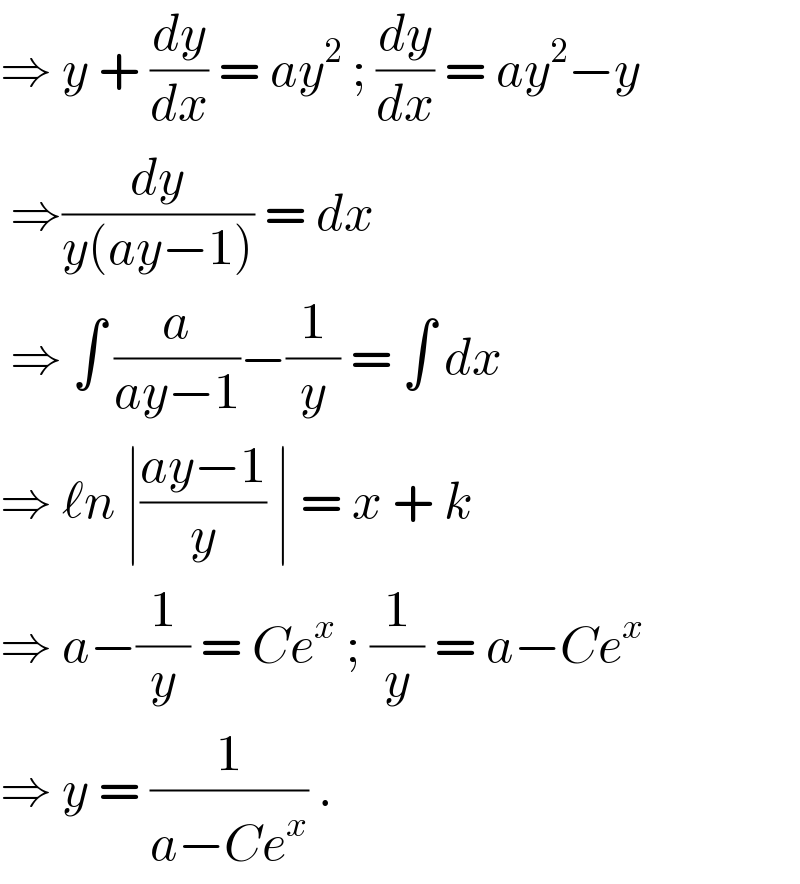
$$\Rightarrow\:{y}\:+\:\frac{{dy}}{{dx}}\:=\:{ay}^{\mathrm{2}} \:;\:\frac{{dy}}{{dx}}\:=\:{ay}^{\mathrm{2}} −{y} \\ $$$$\:\Rightarrow\frac{{dy}}{{y}\left({ay}−\mathrm{1}\right)}\:=\:{dx}\: \\ $$$$\:\Rightarrow\:\int\:\frac{{a}}{{ay}−\mathrm{1}}−\frac{\mathrm{1}}{{y}}\:=\:\int\:{dx} \\ $$$$\Rightarrow\:\ell{n}\:\mid\frac{{ay}−\mathrm{1}}{{y}}\:\mid\:=\:{x}\:+\:{k}\: \\ $$$$\Rightarrow\:{a}−\frac{\mathrm{1}}{{y}}\:=\:{Ce}^{{x}} \:;\:\frac{\mathrm{1}}{{y}}\:=\:{a}−{Ce}^{{x}} \\ $$$$\Rightarrow\:{y}\:=\:\frac{\mathrm{1}}{{a}−{Ce}^{{x}} }\:. \\ $$
