Question Number 108238 by Study last updated on 15/Aug/20

$${y}={e}^{{x}} {ln}\left({sin}\mathrm{2}{x}\right)\:\:\:\:\:\:\:\:\:\:\:\frac{{dy}}{{dx}}=?? \\ $$
Answered by Dwaipayan Shikari last updated on 15/Aug/20

$$\frac{{dy}}{{dx}}={e}^{{x}} {log}\left({sin}\mathrm{2}{x}\right)+\mathrm{2}{e}^{{x}} \frac{{cos}\mathrm{2}{x}}{{sin}\mathrm{2}{x}} \\ $$$$\frac{{dy}}{{dx}}={e}^{{x}} \left({log}\left({sin}\mathrm{2}{x}\right)+\mathrm{2}{cot}\mathrm{2}{x}\right) \\ $$
Answered by john santu last updated on 15/Aug/20
![((♥JS♥)/�) (dy/dx) = e^x ln (sin 2x)+e^x (((2cos 2x)/(sin 2x))) = e^x [ ln (sin 2x)+2 cot 2x ]](https://www.tinkutara.com/question/Q108246.png)
$$\:\:\frac{\heartsuit{JS}\heartsuit}{�} \\ $$$$\frac{{dy}}{{dx}}\:=\:{e}^{{x}} \:\mathrm{ln}\:\left(\mathrm{sin}\:\mathrm{2}{x}\right)+{e}^{{x}} \left(\frac{\mathrm{2cos}\:\mathrm{2}{x}}{\mathrm{sin}\:\mathrm{2}{x}}\right) \\ $$$$=\:{e}^{{x}} \:\left[\:\mathrm{ln}\:\left(\mathrm{sin}\:\mathrm{2}{x}\right)+\mathrm{2}\:\mathrm{cot}\:\mathrm{2}{x}\:\right]\: \\ $$
Answered by mathdave last updated on 15/Aug/20

$${solution} \\ $$$$\frac{{dy}}{{dx}}={e}^{{x}} \bullet\mathrm{2}\frac{\mathrm{cos2}{x}}{\mathrm{sin2}{x}}+{e}^{{x}} \mathrm{ln}\left(\mathrm{sin2}{x}\right) \\ $$$$\frac{{dy}}{{dx}}−{y}=\mathrm{2}{e}^{{x}} \mathrm{cot2}{x} \\ $$
Answered by mathmax by abdo last updated on 15/Aug/20
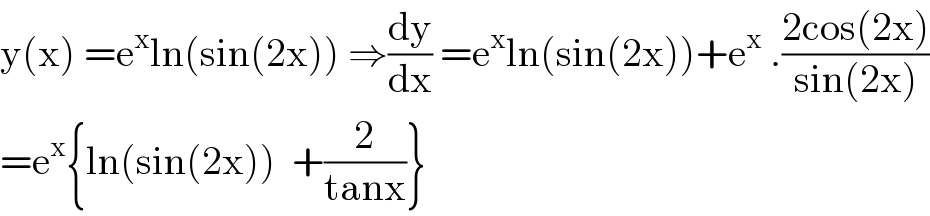
$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{e}^{\mathrm{x}} \mathrm{ln}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right)\:\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}\:=\mathrm{e}^{\mathrm{x}} \mathrm{ln}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right)+\mathrm{e}^{\mathrm{x}} \:.\frac{\mathrm{2cos}\left(\mathrm{2x}\right)}{\mathrm{sin}\left(\mathrm{2x}\right)} \\ $$$$=\mathrm{e}^{\mathrm{x}} \left\{\mathrm{ln}\left(\mathrm{sin}\left(\mathrm{2x}\right)\right)\:\:+\frac{\mathrm{2}}{\mathrm{tanx}}\right\} \\ $$
