Question Number 153033 by ZiYangLee last updated on 04/Sep/21

$${y}=\mathrm{log}\:\left(\mathrm{1}+\mathrm{cos}\:{x}\right) \\ $$$$\frac{{dy}}{{dx}}= \\ $$
Answered by puissant last updated on 04/Sep/21

$${y}={ln}\left(\mathrm{1}+{cosx}\right) \\ $$$$\frac{{dy}}{{dx}}=\frac{−{sinx}}{\mathrm{1}+{cosx}} \\ $$
Answered by physicstutes last updated on 04/Sep/21
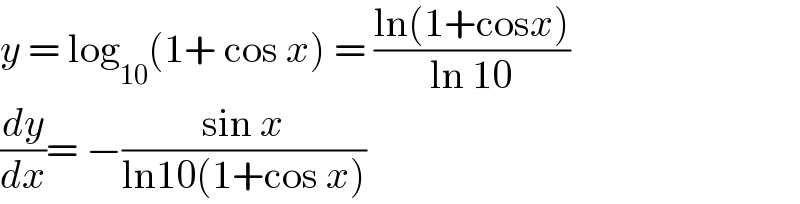
$${y}\:=\:\mathrm{log}_{\mathrm{10}} \left(\mathrm{1}+\:\mathrm{cos}\:{x}\right)\:=\:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{cos}{x}\right)}{\mathrm{ln}\:\mathrm{10}} \\ $$$$\frac{{dy}}{{dx}}=\:−\frac{\mathrm{sin}\:{x}}{\mathrm{ln10}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)} \\ $$
Commented by puissant last updated on 04/Sep/21
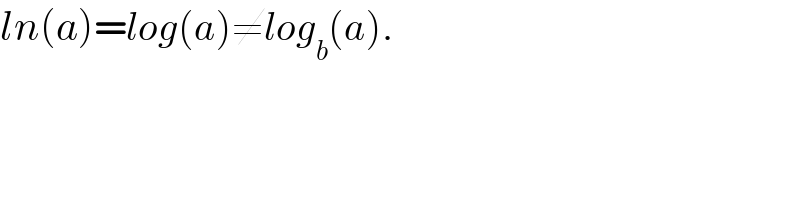
$${ln}\left({a}\right)={log}\left({a}\right)\neq{log}_{{b}} \left({a}\right). \\ $$
Commented by Jonathanwaweh last updated on 05/Sep/21
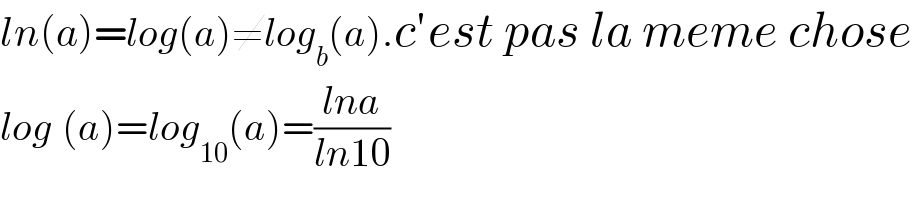
$${ln}\left({a}\right)={log}\left({a}\right)\neq{log}_{{b}} \left({a}\right).{c}'{est}\:{pas}\:{la}\:{meme}\:{chose} \\ $$$${log}_{} \left({a}\right)={log}_{\mathrm{10}} \left({a}\right)=\frac{{lna}}{{ln}\mathrm{10}} \\ $$
Commented by puissant last updated on 10/Sep/21

$${log}\left({a}\right)={ln}\left({a}\right)\:{car}\:{log}\:{c}'{est}\:{en}\:{anglais} \\ $$$${et}\:{ln}\:{c}'{est}\:{en}\:{francais}\:{tous}\:{simplement} \\ $$
