Question Number 124956 by liberty last updated on 07/Dec/20

$$\:{y}\:=\:\mathrm{sec}^{−\mathrm{1}} \left({e}^{{x}^{\mathrm{4}} } \right)\:.\:{Find}\:{dy}\:=? \\ $$
Answered by bemath last updated on 07/Dec/20
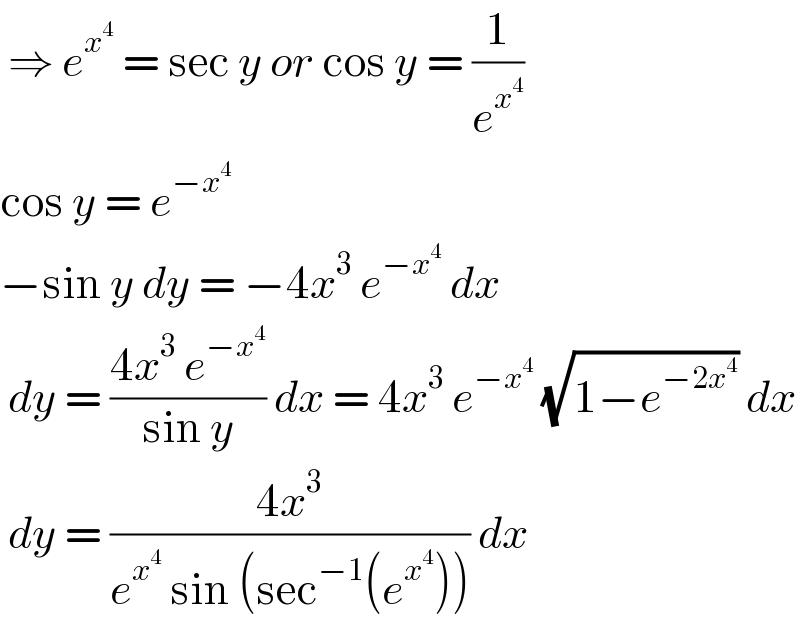
$$\:\Rightarrow\:{e}^{{x}^{\mathrm{4}} } \:=\:\mathrm{sec}\:{y}\:{or}\:\mathrm{cos}\:{y}\:=\:\frac{\mathrm{1}}{{e}^{{x}^{\mathrm{4}} } } \\ $$$$\mathrm{cos}\:{y}\:=\:{e}^{−{x}^{\mathrm{4}} } \\ $$$$−\mathrm{sin}\:{y}\:{dy}\:=\:−\mathrm{4}{x}^{\mathrm{3}} \:{e}^{−{x}^{\mathrm{4}} } \:{dx} \\ $$$$\:{dy}\:=\:\frac{\mathrm{4}{x}^{\mathrm{3}} \:{e}^{−{x}^{\mathrm{4}} } }{\mathrm{sin}\:{y}}\:{dx}\:=\:\mathrm{4}{x}^{\mathrm{3}} \:{e}^{−{x}^{\mathrm{4}} } \:\sqrt{\mathrm{1}−{e}^{−\mathrm{2}{x}^{\mathrm{4}} } }\:{dx}\: \\ $$$$\:{dy}\:=\:\frac{\mathrm{4}{x}^{\mathrm{3}} }{{e}^{{x}^{\mathrm{4}} } \:\mathrm{sin}\:\left(\mathrm{sec}^{−\mathrm{1}} \left({e}^{{x}^{\mathrm{4}} } \right)\right)}\:{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 07/Dec/20
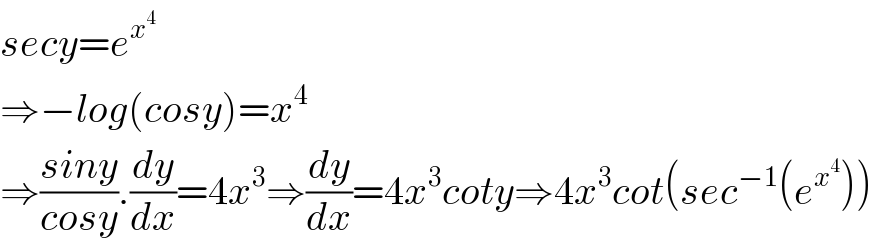
$${secy}={e}^{{x}^{\mathrm{4}} } \\ $$$$\Rightarrow−{log}\left({cosy}\right)={x}^{\mathrm{4}} \\ $$$$\Rightarrow\frac{{siny}}{{cosy}}.\frac{{dy}}{{dx}}=\mathrm{4}{x}^{\mathrm{3}} \Rightarrow\frac{{dy}}{{dx}}=\mathrm{4}{x}^{\mathrm{3}} {coty}\Rightarrow\mathrm{4}{x}^{\mathrm{3}} {cot}\left({sec}^{−\mathrm{1}} \left({e}^{{x}^{\mathrm{4}} } \right)\right) \\ $$
