Menu Close

y-sin-cos-3-x-cos-sin-3-d-2-y-dx-2-

Tinku Tara 0 Comments
Pin




Question Number 130918 by bramlexs22 last updated on 30/Jan/21
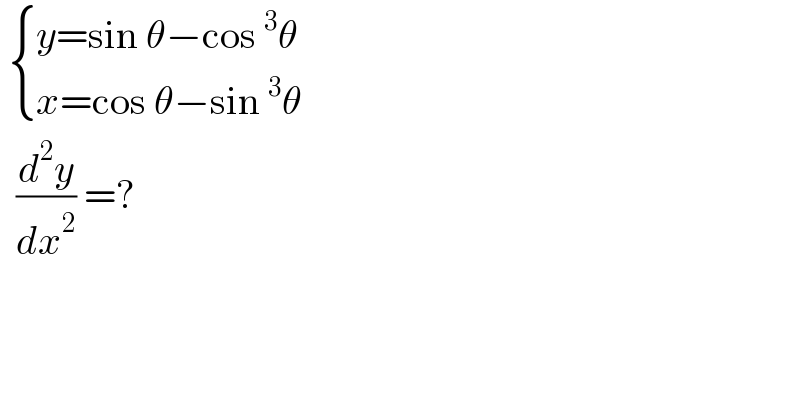
{ ((y=sin θ−cos^3 θ)),((x=cos θ−sin^3 θ)) :} (d^2 y/dx^2 ) =?
$$\:\begin{cases}{{y}=\mathrm{sin}\:\theta−\mathrm{cos}\:^{\mathrm{3}} \theta}\\{{x}=\mathrm{cos}\:\theta−\mathrm{sin}\:^{\mathrm{3}} \theta}\end{cases} \\ $$$$\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=? \\ $$
Answered by benjo_mathlover last updated on 30/Jan/21
{ (((dy/dθ)=cos θ+3cos^2 θ sin θ)),(((dx/dθ) = −sin θ−3sin^2 θ cos θ)) :} (dy/dx) = (dy/dθ) . (dθ/dx) = ((cos θ+3cos^2 θ sin θ)/(−sin θ−3sin^2 θ cos θ)) = ((cos θ(1+3cos θsin θ))/(−sin θ(1+3cos θ sin θ)))=−cot θ (d^2 y/dx^2 ) = (d/dθ)(−cot θ). (dθ/dx) = csc^2 θ .((1/(−sin θ−3sin^2 θ cos θ))) = −(1/(sin^3 θ(1+(3/2)sin 2θ))) = −(2/(sin^3 θ(2+3sin 2θ)))
$$\:\:\begin{cases}{\frac{\mathrm{dy}}{\mathrm{d}\theta}=\mathrm{cos}\:\theta+\mathrm{3cos}\:^{\mathrm{2}} \theta\:\mathrm{sin}\:\theta}\\{\frac{\mathrm{dx}}{\mathrm{d}\theta}\:=\:−\mathrm{sin}\:\theta−\mathrm{3sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:\theta}\end{cases} \\ $$$$\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{dy}}{\mathrm{d}\theta}\:.\:\frac{\mathrm{d}\theta}{\mathrm{dx}}\:=\:\frac{\mathrm{cos}\:\theta+\mathrm{3cos}\:^{\mathrm{2}} \theta\:\mathrm{sin}\:\theta}{−\mathrm{sin}\:\theta−\mathrm{3sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:\theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{cos}\:\theta\left(\mathrm{1}+\mathrm{3cos}\:\theta\mathrm{sin}\:\theta\right)}{−\mathrm{sin}\:\theta\left(\mathrm{1}+\mathrm{3cos}\:\theta\:\mathrm{sin}\:\theta\right)}=−\mathrm{cot}\:\theta \\ $$$$\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:\frac{\mathrm{d}}{\mathrm{d}\theta}\left(−\mathrm{cot}\:\theta\right).\:\frac{\mathrm{d}\theta}{\mathrm{dx}}\:=\:\mathrm{csc}^{\mathrm{2}} \theta\:.\left(\frac{\mathrm{1}}{−\mathrm{sin}\:\theta−\mathrm{3sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:\theta}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{sin}\:^{\mathrm{3}} \theta\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\frac{\mathrm{2}}{\mathrm{sin}\:^{\mathrm{3}} \theta\left(\mathrm{2}+\mathrm{3sin}\:\mathrm{2}\theta\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *