Question Number 95748 by bobhans last updated on 27/May/20
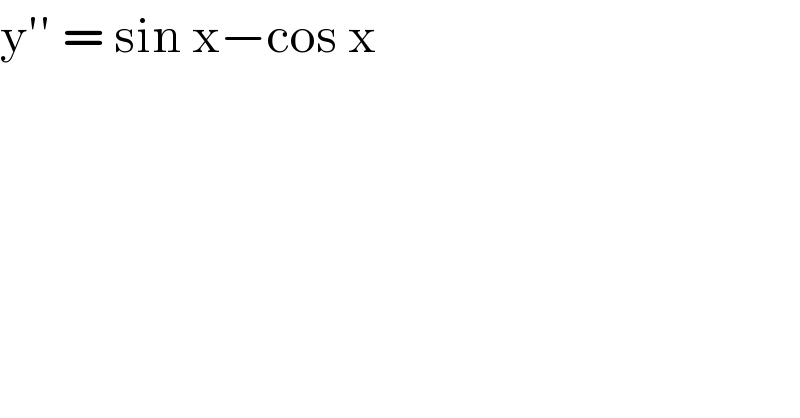
$$\mathrm{y}''\:=\:\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x} \\ $$
Answered by mathmax by abdo last updated on 27/May/20
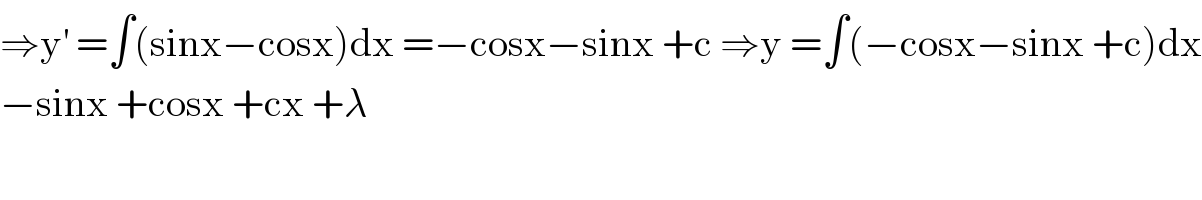
$$\Rightarrow\mathrm{y}^{'} \:=\int\left(\mathrm{sinx}−\mathrm{cosx}\right)\mathrm{dx}\:=−\mathrm{cosx}−\mathrm{sinx}\:+\mathrm{c}\:\Rightarrow\mathrm{y}\:=\int\left(−\mathrm{cosx}−\mathrm{sinx}\:+\mathrm{c}\right)\mathrm{dx} \\ $$$$−\mathrm{sinx}\:+\mathrm{cosx}\:+\mathrm{cx}\:+\lambda \\ $$
Commented by bobhans last updated on 27/May/20
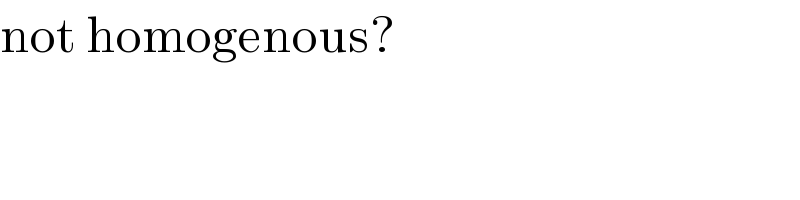
$$\mathrm{not}\:\mathrm{homogenous}? \\ $$
Answered by bobhans last updated on 27/May/20
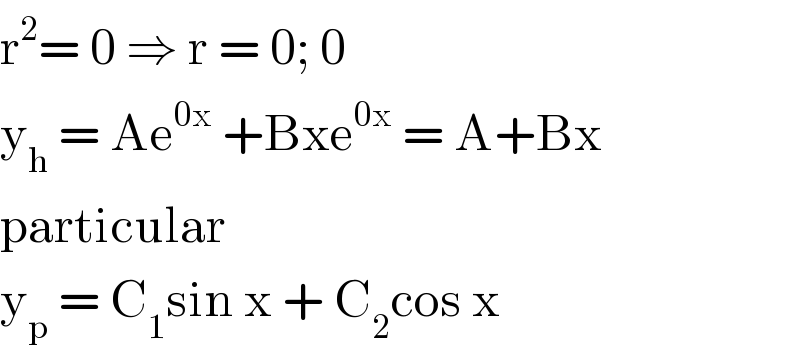
$$\mathrm{r}^{\mathrm{2}} =\:\mathrm{0}\:\Rightarrow\:\mathrm{r}\:=\:\mathrm{0};\:\mathrm{0} \\ $$$$\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{Ae}^{\mathrm{0x}} \:+\mathrm{Bxe}^{\mathrm{0x}} \:=\:\mathrm{A}+\mathrm{Bx}\: \\ $$$$\mathrm{particular}\: \\ $$$$\mathrm{y}_{\mathrm{p}} \:=\:\mathrm{C}_{\mathrm{1}} \mathrm{sin}\:\mathrm{x}\:+\:\mathrm{C}_{\mathrm{2}} \mathrm{cos}\:\mathrm{x}\: \\ $$
Commented by mr W last updated on 27/May/20

$${particular}\:{solution}\:{should}\:{have}\:{no} \\ $$$${constant}\:{in}\:{it}!\:{that}'{s}\:{why}\:{it}\:{is}\:{called} \\ $$$$“{particular}''. \\ $$$${in}\:{this}\:{case}\:{it}\:{is}\:−\mathrm{sin}\:{x}+\mathrm{cos}\:{x},\:{not} \\ $$$${C}_{\mathrm{1}} \mathrm{sin}\:{x}+{C}_{\mathrm{2}} \mathrm{cos}\:{x}. \\ $$
Commented by john santu last updated on 28/May/20
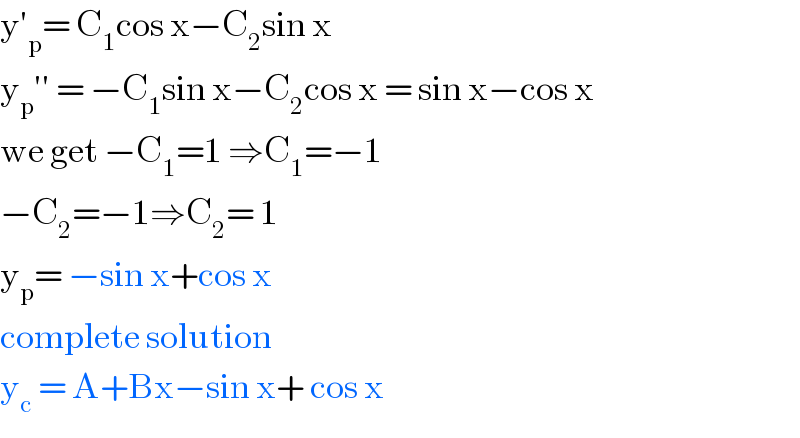
$$\mathrm{y}'_{\mathrm{p}} =\:\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:\mathrm{x}−\mathrm{C}_{\mathrm{2}} \mathrm{sin}\:\mathrm{x}\: \\ $$$$\mathrm{y}_{\mathrm{p}} ''\:=\:−\mathrm{C}_{\mathrm{1}} \mathrm{sin}\:\mathrm{x}−\mathrm{C}_{\mathrm{2}} \mathrm{cos}\:\mathrm{x}\:=\:\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x} \\ $$$$\mathrm{we}\:\mathrm{get}\:−\mathrm{C}_{\mathrm{1}} =\mathrm{1}\:\Rightarrow\mathrm{C}_{\mathrm{1}} =−\mathrm{1} \\ $$$$−\mathrm{C}_{\mathrm{2}} =−\mathrm{1}\Rightarrow\mathrm{C}_{\mathrm{2}} =\:\mathrm{1} \\ $$$$\mathrm{y}_{\mathrm{p}} =\:−\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x} \\ $$$$\mathrm{complete}\:\mathrm{solution} \\ $$$$\mathrm{y}_{\mathrm{c}} \:=\:\mathrm{A}+\mathrm{Bx}−\mathrm{sin}\:\mathrm{x}+\:\mathrm{cos}\:\mathrm{x}\: \\ $$
Commented by mr W last updated on 28/May/20

$${please}\:{recheck}: \\ $$$$−{C}_{\mathrm{1}} =−\mathrm{1}\:\Rightarrow{C}_{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{y}_{\mathrm{p}} =\:−\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x} \\ $$
