Question Number 129595 by Adel last updated on 16/Jan/21

$$\mathrm{y}=\sqrt{\mathrm{sin}\:\mathrm{x}+\sqrt{\mathrm{sin}\:\mathrm{x}+\sqrt{\mathrm{sin}\:\mathrm{x}+………….\infty}}} \\ $$$$ \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=? \\ $$
Answered by ajfour last updated on 16/Jan/21
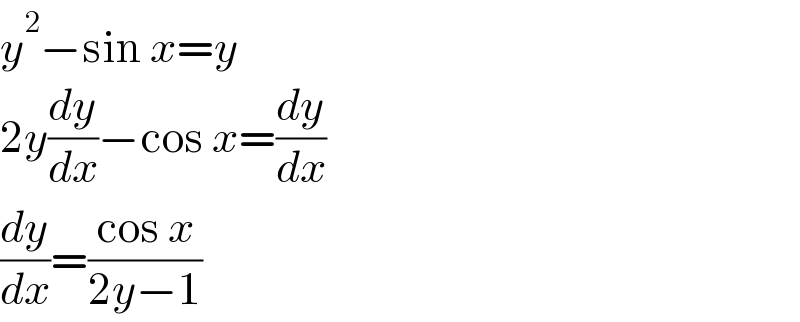
$${y}^{\mathrm{2}} −\mathrm{sin}\:{x}={y} \\ $$$$\mathrm{2}{y}\frac{{dy}}{{dx}}−\mathrm{cos}\:{x}=\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{cos}\:{x}}{\mathrm{2}{y}−\mathrm{1}} \\ $$
Answered by mr W last updated on 16/Jan/21
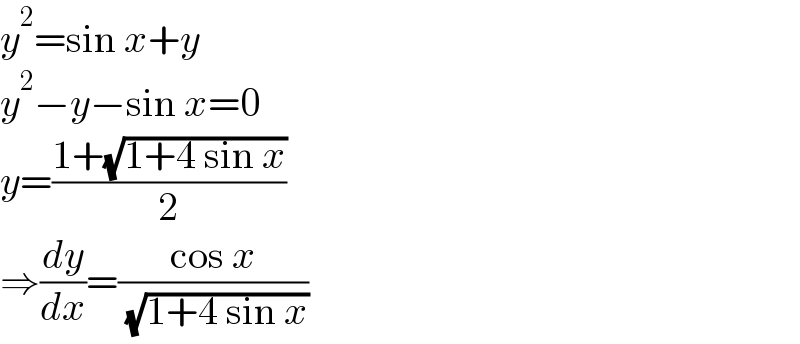
$${y}^{\mathrm{2}} =\mathrm{sin}\:{x}+{y} \\ $$$${y}^{\mathrm{2}} −{y}−\mathrm{sin}\:{x}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}\:\mathrm{sin}\:{x}}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{1}+\mathrm{4}\:\mathrm{sin}\:{x}}} \\ $$
