Question Number 122379 by bounhome last updated on 16/Nov/20
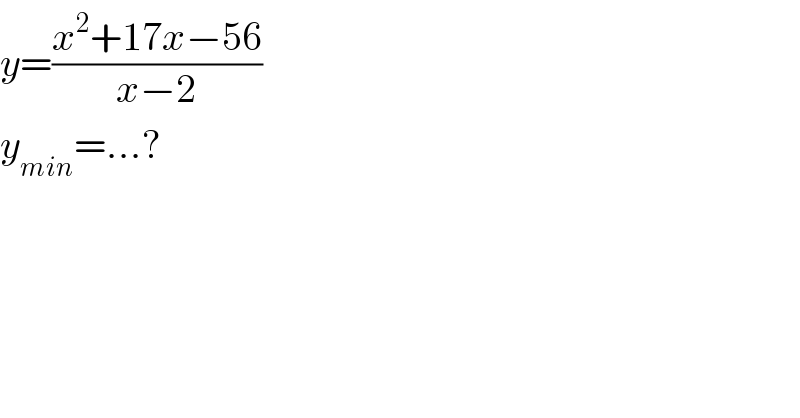
$${y}=\frac{{x}^{\mathrm{2}} +\mathrm{17}{x}−\mathrm{56}}{{x}−\mathrm{2}} \\ $$$${y}_{{min}} =…? \\ $$
Answered by MJS_new last updated on 16/Nov/20
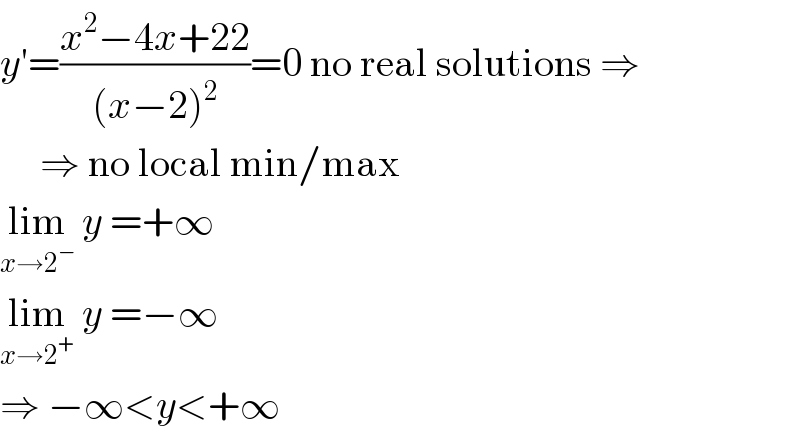
$${y}'=\frac{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{22}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{0}\:\mathrm{no}\:\mathrm{real}\:\mathrm{solutions}\:\Rightarrow\: \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{no}\:\mathrm{local}\:\mathrm{min}/\mathrm{max} \\ $$$$\underset{{x}\rightarrow\mathrm{2}^{−} } {\mathrm{lim}}\:{y}\:=+\infty \\ $$$$\underset{{x}\rightarrow\mathrm{2}^{+} } {\mathrm{lim}}\:{y}\:=−\infty \\ $$$$\Rightarrow\:−\infty<{y}<+\infty \\ $$
