Question Number 90262 by jagoll last updated on 22/Apr/20
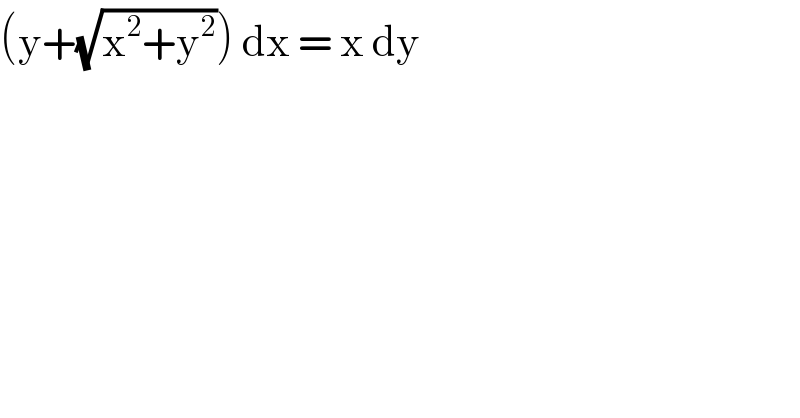
$$\left(\mathrm{y}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\right)\:\mathrm{dx}\:=\:\mathrm{x}\:\mathrm{dy}\: \\ $$
Commented by john santu last updated on 22/Apr/20
![((y/x)+(√(1+((y/x))^2 ))) dx = dy [ y = px ⇒dy = p dx + x dp ] (p +(√(1+p^2 ))) dx = p dx + x dp (√(1+p^2 )) dx = x dp (dx/x) = (dp/( (√(1+p^2 )))) let I = ∫ (dp/( (√(1+p^2 )))) , [ p = tan u ] I = ∫ ((sec^2 u du)/(sec u)) = ln ∣sec u+tan u∣ ⇒ ln∣Cx∣ = ln∣ sec u+tan u∣ Cx = p+(√(1+p^2 )) Cx = ((y+(√(x^2 +y^2 )))/x) Cx^2 = y +(√(x^2 +y^2 ))](https://www.tinkutara.com/question/Q90263.png)
$$\left(\frac{{y}}{{x}}+\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\right)\:{dx}\:=\:{dy}\: \\ $$$$\left[\:{y}\:=\:{px}\:\Rightarrow{dy}\:=\:{p}\:{dx}\:+\:{x}\:{dp}\:\right]\: \\ $$$$\left({p}\:+\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }\right)\:{dx}\:=\:{p}\:{dx}\:+\:{x}\:{dp}\: \\ $$$$\sqrt{\mathrm{1}+{p}^{\mathrm{2}} \:}\:{dx}\:=\:{x}\:{dp}\: \\ $$$$\frac{{dx}}{{x}}\:=\:\frac{{dp}}{\:\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}\: \\ $$$${let}\:{I}\:=\:\int\:\frac{{dp}}{\:\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}\:,\:\left[\:{p}\:=\:\mathrm{tan}\:{u}\:\right] \\ $$$${I}\:=\:\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} {u}\:{du}}{\mathrm{sec}\:{u}}\:=\:\mathrm{ln}\:\mid\mathrm{sec}\:{u}+\mathrm{tan}\:{u}\mid \\ $$$$\Rightarrow\:\mathrm{ln}\mid{Cx}\mid\:=\:\mathrm{ln}\mid\:\mathrm{sec}\:{u}+\mathrm{tan}\:{u}\mid \\ $$$${Cx}\:=\:{p}+\sqrt{\mathrm{1}+{p}^{\mathrm{2}} } \\ $$$${Cx}\:=\:\frac{{y}+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}{{x}}\:\: \\ $$$${Cx}^{\mathrm{2}} \:=\:{y}\:+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\: \\ $$$$ \\ $$
Commented by jagoll last updated on 22/Apr/20

$$\mathrm{waw}..\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$
Answered by ajfour last updated on 22/Apr/20
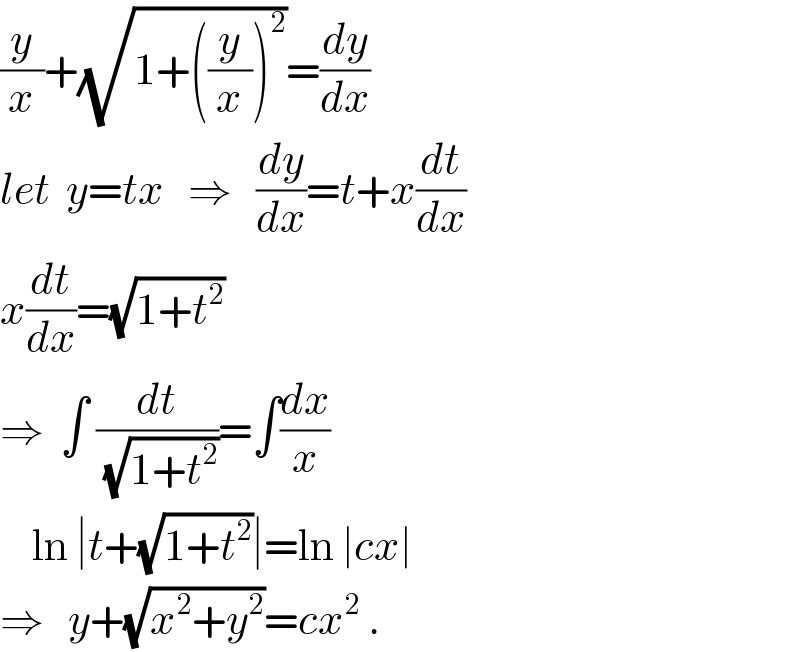
$$\frac{{y}}{{x}}+\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }=\frac{{dy}}{{dx}} \\ $$$${let}\:\:{y}={tx}\:\:\:\Rightarrow\:\:\:\frac{{dy}}{{dx}}={t}+{x}\frac{{dt}}{{dx}} \\ $$$${x}\frac{{dt}}{{dx}}=\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\int\:\frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}=\int\frac{{dx}}{{x}} \\ $$$$\:\:\:\:\mathrm{ln}\:\mid{t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\mid=\mathrm{ln}\:\mid{cx}\mid \\ $$$$\Rightarrow\:\:\:{y}+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }={cx}^{\mathrm{2}} \:. \\ $$
Answered by TANMAY PANACEA. last updated on 22/Apr/20
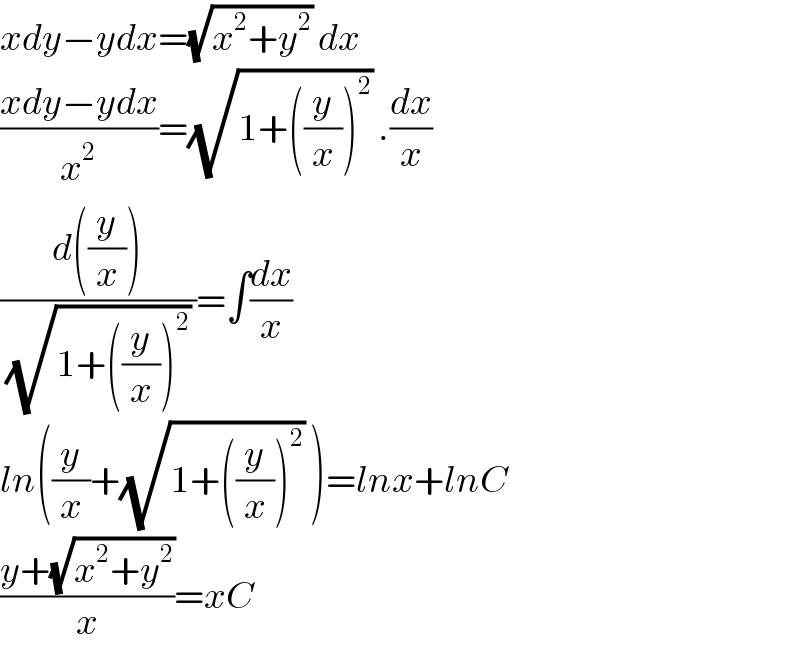
$${xdy}−{ydx}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:{dx} \\ $$$$\frac{{xdy}−{ydx}}{{x}^{\mathrm{2}} }=\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:.\frac{{dx}}{{x}} \\ $$$$\frac{{d}\left(\frac{{y}}{{x}}\right)}{\:\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:}=\int\frac{{dx}}{{x}} \\ $$$${ln}\left(\frac{{y}}{{x}}+\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:\right)={lnx}+{lnC} \\ $$$$\frac{{y}+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}{{x}}={xC} \\ $$
