Menu Close

y-x-2-y-2-dx-x-x-x-2-y-2-dy-0-

Tinku Tara 0 Comments
Pin




Question Number 121609 by benjo_mathlover last updated on 10/Nov/20
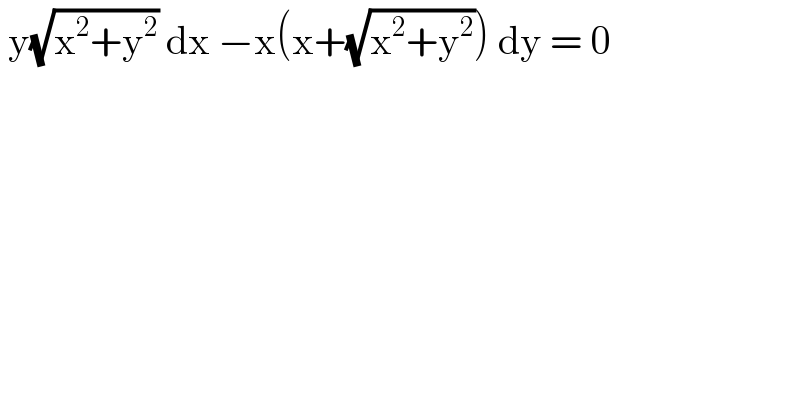
y(√(x^2 +y^2 )) dx −x(x+(√(x^2 +y^2 ))) dy = 0
$$\:\mathrm{y}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\:\mathrm{dx}\:−\mathrm{x}\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\right)\:\mathrm{dy}\:=\:\mathrm{0}\: \\ $$$$ \\ $$
Answered by liberty last updated on 10/Nov/20
(dy/dx) = ((y(√(x^2 +y^2 )))/(x(x+(√(x^2 +y^2 ))))) let y = vx ⇒(dy/dx) = v + x (dv/dx) ⇒ v + x (dv/dx) = ((vx (√(x^2 +v^2 x^2 )))/(x^2 +x(√(x^2 +v^2 x^2 )))) ⇒v + x (dv/dx) = ((v(√(1+v^2 )))/(1+(√(1+v^2 )))) ⇒x (dv/dx) = ((v(√(1+v^2 ))−v−v(√(1+v^2 )))/(1+(√(1+v^2 )))) ⇒ (((1+(√(1+v^2 ))))/v) dv = − (dx/x) ⇒ ln ∣v∣ + ∫ (((√(1+v^2 )) dv)/v) = −ln ∣x∣ + c let I = ∫ ((√(1+v^2 ))/v) dv = ∫ ((1+v^2 )/(v(√(1+v^2 )))) dv I = ∫ (dv/(v(√(1+v^2 )))) + ∫ (v/( (√(1+v^2 )))) dv I = (1/2)∫ ((d(1+v^2 ))/( (√(1+v^2 ))))+ ∫ ((sec^2 u du)/(tan u. sec u)) [ u=arc tan v ] I=(√(1+v^2 )) + ∫ csc u du I= (√(1+v^2 )) + ln ∣ csc u−cot u ∣ ∴ the solution ln ∣vx∣ + (√(1+v^2 )) + ln ∣(((√(1+v^2 )) −1)/v) ∣ = C ln ∣x((((√(x^2 +y^2 ))−x)/x))∣+ ((√(x^2 +y^2 ))/x) = C ln ∣ (√(x^2 +y^2 ))−x∣ + ((√(x^2 +y^2 ))/x) = C
$$\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{y}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }}{\mathrm{x}\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\right)} \\ $$$$\mathrm{let}\:\mathrm{y}\:=\:\mathrm{vx}\:\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{v}\:+\:\mathrm{x}\:\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\Rightarrow\:\mathrm{v}\:+\:\mathrm{x}\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\frac{\mathrm{vx}\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{v}\:+\:\mathrm{x}\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\frac{\mathrm{v}\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{x}\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\frac{\mathrm{v}\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }−\mathrm{v}−\mathrm{v}\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }\right)}{\mathrm{v}}\:\mathrm{dv}\:=\:−\:\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$\Rightarrow\:\mathrm{ln}\:\mid\mathrm{v}\mid\:+\:\int\:\frac{\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }\:\mathrm{dv}}{\mathrm{v}}\:=\:−\mathrm{ln}\:\mid\mathrm{x}\mid\:+\:\mathrm{c}\: \\ $$$$\mathrm{let}\:\mathrm{I}\:=\:\int\:\frac{\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }}{\mathrm{v}}\:\mathrm{dv}\:=\:\int\:\frac{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }{\mathrm{v}\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }}\:\mathrm{dv} \\ $$$$\mathrm{I}\:=\:\int\:\frac{\mathrm{dv}}{\mathrm{v}\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }}\:+\:\int\:\frac{\mathrm{v}}{\:\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }}\:\mathrm{dv} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{1}+\mathrm{v}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }}+\:\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{u}\:\mathrm{du}}{\mathrm{tan}\:\mathrm{u}.\:\mathrm{sec}\:\mathrm{u}}\:\left[\:\mathrm{u}=\mathrm{arc}\:\mathrm{tan}\:\mathrm{v}\:\right] \\ $$$$\mathrm{I}=\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }\:+\:\int\:\mathrm{csc}\:\mathrm{u}\:\mathrm{du}\: \\ $$$$\mathrm{I}=\:\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }\:+\:\mathrm{ln}\:\mid\:\mathrm{csc}\:\mathrm{u}−\mathrm{cot}\:\mathrm{u}\:\mid\: \\ $$$$ \\ $$$$\therefore\:\mathrm{the}\:\mathrm{solution} \\ $$$$\mathrm{ln}\:\mid\mathrm{vx}\mid\:+\:\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }\:+\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{1}+\mathrm{v}^{\mathrm{2}} }\:−\mathrm{1}}{\mathrm{v}}\:\mid\:=\:\mathrm{C} \\ $$$$\mathrm{ln}\:\mid\mathrm{x}\left(\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }−\mathrm{x}}{\mathrm{x}}\right)\mid+\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }}{\mathrm{x}}\:=\:\mathrm{C} \\ $$$$\mathrm{ln}\:\mid\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }−\mathrm{x}\mid\:+\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }}{\mathrm{x}}\:=\:\mathrm{C} \\ $$$$ \\ $$
Answered by TANMAY PANACEA last updated on 10/Nov/20
y(√(x^2 +y^2 )) dx−x(√(x^2 +y^2 )) dy−x^2 dy=0 −(√(x^2 +y^2 )) (xdy−ydx)=x^2 dy −x×(√(1+((y/x))^2 )) ×(((xdy−ydx)/x^2 ))=dy −((x/y))(√(1+((y/x))^2 )) ×d((y/x))=(dy/y) (dy/y)+((x/y))(√(1+((y/x))^2 )) ×d((y/x))=0=dC (dy/y)+(((√(1+p^2 )) dp)/p)=dC ★intregation ∫(dy/y)=lny+C_1 ■∫((√(1+p^2 ))/p)dp →k^2 =1+p^2 →kdk=pdp ∫((√(1+p^2 ))/p^2 )×pdp→∫((k×kdk)/((k^2 −1)))=∫((k^2 −1+1)/(k^2 −1))dk=∫(1+(1/(k^2 −1))))dk =k+(1/2)ln(((k−1)/(k+1)))+C_2 =(√(1+p^2 )) +(1/2)ln((((√(1+p^2 )) −1)/( (√(1+p^2 )) +1)))+C_2 lny+(√(1+p^2 )) +(1/2)ln((((√(1+p^2 )) −1)/( (√(1+p^2 )) +1)))=C lny+(√(1+((y/x))^2 )) +(1/2)ln((((√(1+((y/x))^2 −1)) )/( (√(1+((y/x))^2 )) +1)))=C
$${y}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:{dx}−{x}\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:{dy}−{x}^{\mathrm{2}} {dy}=\mathrm{0} \\ $$$$−\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\left({xdy}−{ydx}\right)={x}^{\mathrm{2}} {dy} \\ $$$$−{x}×\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:×\left(\frac{{xdy}−{ydx}}{{x}^{\mathrm{2}} }\right)={dy} \\ $$$$−\left(\frac{{x}}{{y}}\right)\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:×{d}\left(\frac{{y}}{{x}}\right)=\frac{{dy}}{{y}} \\ $$$$\frac{{dy}}{{y}}+\left(\frac{{x}}{{y}}\right)\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:×{d}\left(\frac{{y}}{{x}}\right)=\mathrm{0}={dC} \\ $$$$\frac{{dy}}{{y}}+\frac{\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }\:{dp}}{{p}}={dC} \\ $$$$\bigstar{intregation}\:\:\int\frac{{dy}}{{y}}={lny}+{C}_{\mathrm{1}} \\ $$$$\blacksquare\int\frac{\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}{{p}}{dp}\:\rightarrow{k}^{\mathrm{2}} =\mathrm{1}+{p}^{\mathrm{2}} \rightarrow{kdk}={pdp} \\ $$$$\int\frac{\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }}{{p}^{\mathrm{2}} }×{pdp}\rightarrow\int\frac{{k}×{kdk}}{\left({k}^{\mathrm{2}} −\mathrm{1}\right)}=\int\frac{{k}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{k}^{\mathrm{2}} −\mathrm{1}}{dk}=\int\left(\mathrm{1}+\frac{\mathrm{1}}{\left.{k}^{\mathrm{2}} −\mathrm{1}\right)}\right){dk} \\ $$$$={k}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}\right)+{C}_{\mathrm{2}} \\ $$$$=\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }\:−\mathrm{1}}{\:\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }\:+\mathrm{1}}\right)+\mathrm{C}_{\mathrm{2}} \\ $$$${lny}+\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }\:−\mathrm{1}}{\:\sqrt{\mathrm{1}+{p}^{\mathrm{2}} }\:+\mathrm{1}}\right)={C} \\ $$$${lny}+\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}}\:}{\:\sqrt{\mathrm{1}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} }\:+\mathrm{1}}\right)={C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *