Question Number 184019 by HeferH last updated on 02/Jan/23

$$\begin{cases}{{y}^{{x}} =\:\mathrm{64}}\\{{y}^{\frac{{x}\:+\:\mathrm{1}}{{x}\:−\:\mathrm{1}}} \:=\:\mathrm{16}}\end{cases} \\ $$$$\:{find}\:“{x}'' \\ $$
Commented by a.lgnaoui last updated on 02/Jan/23
$${Hapy}\:{New}\:{year} \\ $$
Commented by Gazella thomsonii last updated on 02/Jan/23

$$=\mathrm{Ha}^{\mathrm{2}} \mathrm{e}^{\mathrm{2}} \mathrm{p}^{\mathrm{2}} \mathrm{wy}^{\mathrm{2}} \mathrm{r} \\ $$
Answered by manolex last updated on 02/Jan/23
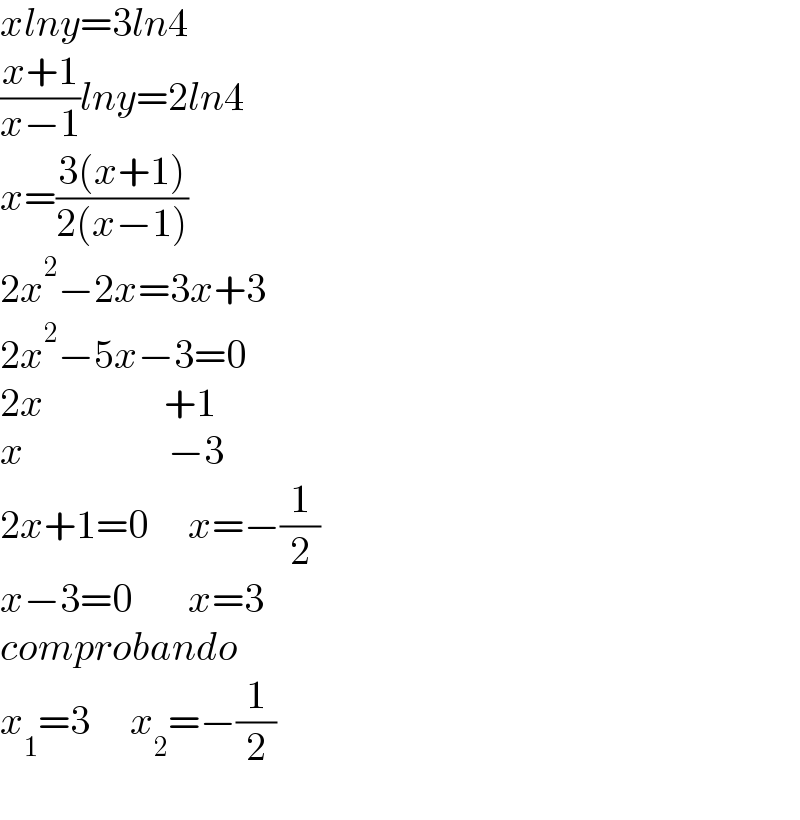
$${xlny}=\mathrm{3}{ln}\mathrm{4} \\ $$$$\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}{lny}=\mathrm{2}{ln}\mathrm{4} \\ $$$${x}=\frac{\mathrm{3}\left({x}+\mathrm{1}\right)}{\mathrm{2}\left({x}−\mathrm{1}\right)} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}=\mathrm{3}{x}+\mathrm{3} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{2}{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{1} \\ $$$${x}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3} \\ $$$$\mathrm{2}{x}+\mathrm{1}=\mathrm{0}\:\:\:\:\:{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${x}−\mathrm{3}=\mathrm{0}\:\:\:\:\:\:\:{x}=\mathrm{3} \\ $$$${comprobando} \\ $$$${x}_{\mathrm{1}} =\mathrm{3}\:\:\:\:\:{x}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by manolex last updated on 02/Jan/23
$${Happy}\:{new}\:{year},{Sr}.{HeferH} \\ $$
Commented by HeferH last updated on 02/Jan/23

$${Happy}\:{new}\:{year}\:! \\ $$$$\left.\::\right) \\ $$
