Question Number 129222 by bramlexs22 last updated on 14/Jan/21
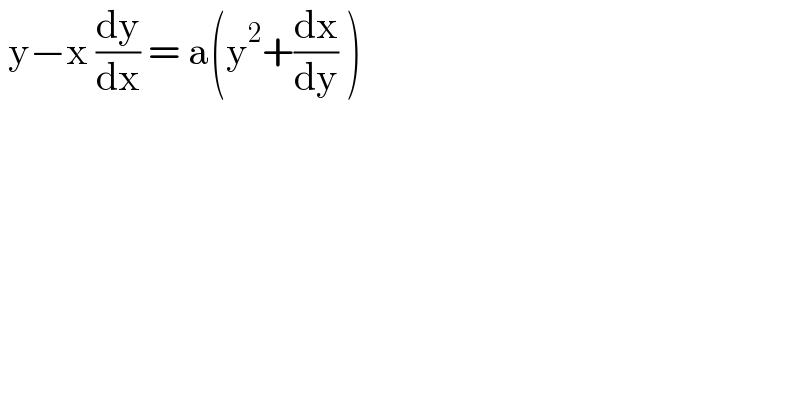
$$\:\mathrm{y}−\mathrm{x}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{a}\left(\mathrm{y}^{\mathrm{2}} +\frac{\mathrm{dx}}{\mathrm{dy}}\:\right) \\ $$
Answered by bobhans last updated on 14/Jan/21
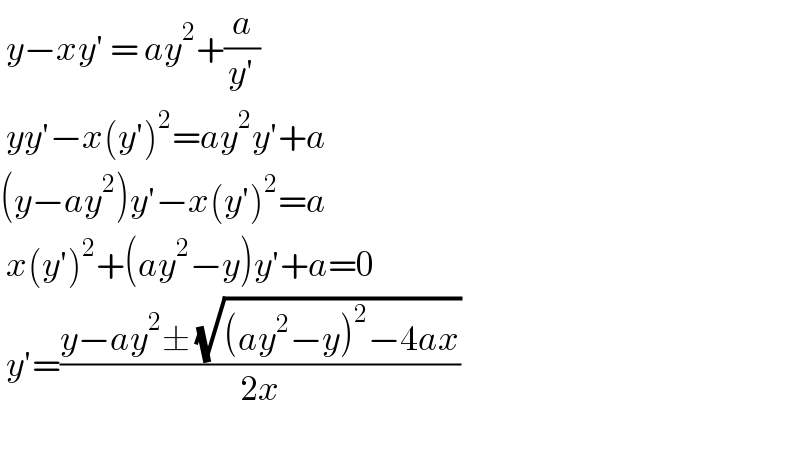
$$\:{y}−{xy}'\:=\:{ay}^{\mathrm{2}} +\frac{{a}}{{y}'} \\ $$$$\:{yy}'−{x}\left({y}'\right)^{\mathrm{2}} ={ay}^{\mathrm{2}} {y}'+{a} \\ $$$$\left({y}−{ay}^{\mathrm{2}} \right){y}'−{x}\left({y}'\right)^{\mathrm{2}} ={a} \\ $$$$\:{x}\left({y}'\right)^{\mathrm{2}} +\left({ay}^{\mathrm{2}} −{y}\right){y}'+{a}=\mathrm{0} \\ $$$$\:{y}'=\frac{{y}−{ay}^{\mathrm{2}} \pm\:\sqrt{\left({ay}^{\mathrm{2}} −{y}\right)^{\mathrm{2}} −\mathrm{4}{ax}}}{\mathrm{2}{x}} \\ $$$$ \\ $$
