Question Number 123282 by zarminaawan last updated on 24/Nov/20
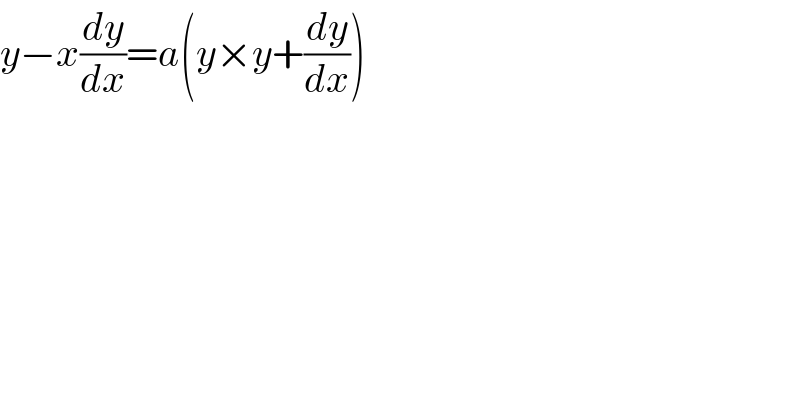
$${y}−{x}\frac{{dy}}{{dx}}={a}\left({y}×{y}+\frac{{dy}}{{dx}}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 24/Nov/20
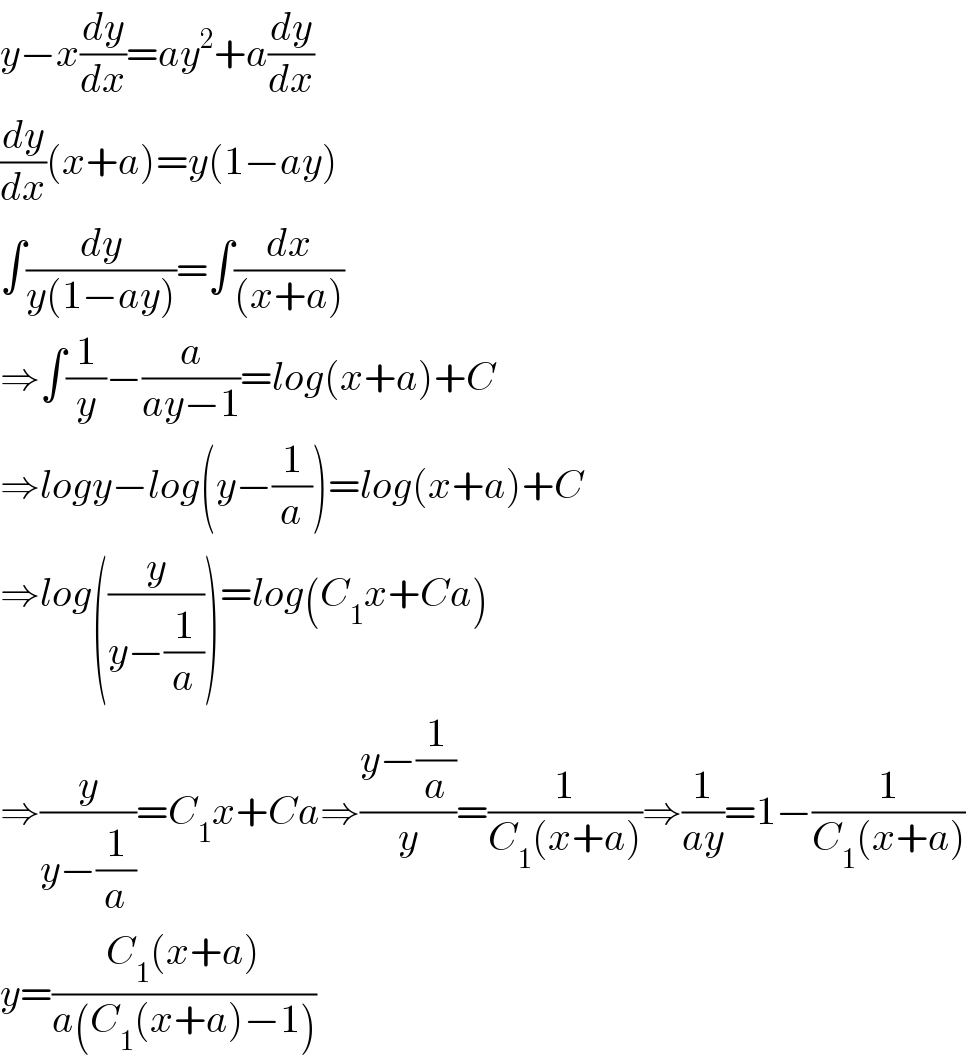
$${y}−{x}\frac{{dy}}{{dx}}={ay}^{\mathrm{2}} +{a}\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}\left({x}+{a}\right)={y}\left(\mathrm{1}−{ay}\right) \\ $$$$\int\frac{{dy}}{{y}\left(\mathrm{1}−{ay}\right)}=\int\frac{{dx}}{\left({x}+{a}\right)}\: \\ $$$$\Rightarrow\int\frac{\mathrm{1}}{{y}}−\frac{{a}}{{ay}−\mathrm{1}}={log}\left({x}+{a}\right)+{C} \\ $$$$\Rightarrow{logy}−{log}\left({y}−\frac{\mathrm{1}}{{a}}\right)={log}\left({x}+{a}\right)+{C} \\ $$$$\Rightarrow{log}\left(\frac{{y}}{{y}−\frac{\mathrm{1}}{{a}}}\right)={log}\left({C}_{\mathrm{1}} {x}+{Ca}\right) \\ $$$$\Rightarrow\frac{{y}}{{y}−\frac{\mathrm{1}}{{a}}}={C}_{\mathrm{1}} {x}+{Ca}\Rightarrow\frac{{y}−\frac{\mathrm{1}}{{a}}}{{y}}=\frac{\mathrm{1}}{{C}_{\mathrm{1}} \left({x}+{a}\right)}\Rightarrow\frac{\mathrm{1}}{{ay}}=\mathrm{1}−\frac{\mathrm{1}}{{C}_{\mathrm{1}} \left({x}+{a}\right)} \\ $$$${y}=\frac{{C}_{\mathrm{1}} \left({x}+{a}\right)}{{a}\left({C}_{\mathrm{1}} \left({x}+{a}\right)−\mathrm{1}\right)} \\ $$
Commented by zarminaawan last updated on 24/Nov/20

$${thankyou}\:{sir} \\ $$
Answered by TANMAY PANACEA last updated on 24/Nov/20
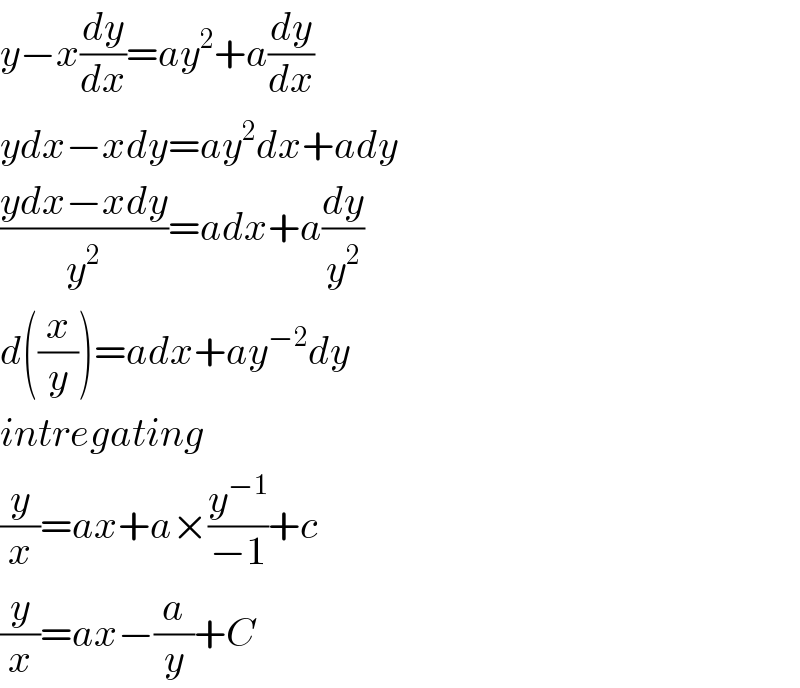
$${y}−{x}\frac{{dy}}{{dx}}={ay}^{\mathrm{2}} +{a}\frac{{dy}}{{dx}} \\ $$$${ydx}−{xdy}={ay}^{\mathrm{2}} {dx}+{ady} \\ $$$$\frac{{ydx}−{xdy}}{{y}^{\mathrm{2}} }={adx}+{a}\frac{{dy}}{{y}^{\mathrm{2}} } \\ $$$${d}\left(\frac{{x}}{{y}}\right)={adx}+{ay}^{−\mathrm{2}} {dy} \\ $$$${intregating} \\ $$$$\frac{{y}}{{x}}={ax}+{a}×\frac{{y}^{−\mathrm{1}} }{−\mathrm{1}}+{c} \\ $$$$\frac{{y}}{{x}}={ax}−\frac{{a}}{{y}}+{C} \\ $$
