Question Number 162675 by Mathematification last updated on 31/Dec/21

$${y}\:=\:\sqrt{{x}} \\ $$$${Find}\:\:\:\frac{{dy}}{{dx}}\:\:{by}\:{first}\:{principle}. \\ $$
Answered by tounghoungko last updated on 31/Dec/21
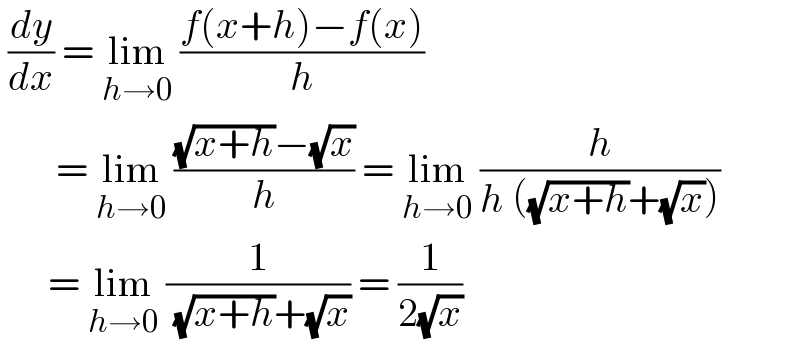
$$\:\frac{{dy}}{{dx}}\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$$$\:\:\:\:\:\:\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}+{h}}−\sqrt{{x}}}{{h}}\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{h}}{{h}\:\left(\sqrt{{x}+{h}}+\sqrt{{x}}\right)} \\ $$$$\:\:\:\:\:\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{{x}+{h}}+\sqrt{{x}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\: \\ $$
