Menu Close

y-x-x-x-dy-dx-

Tinku Tara 0 Comments
Pin




Question Number 109724 by bobhans last updated on 25/Aug/20
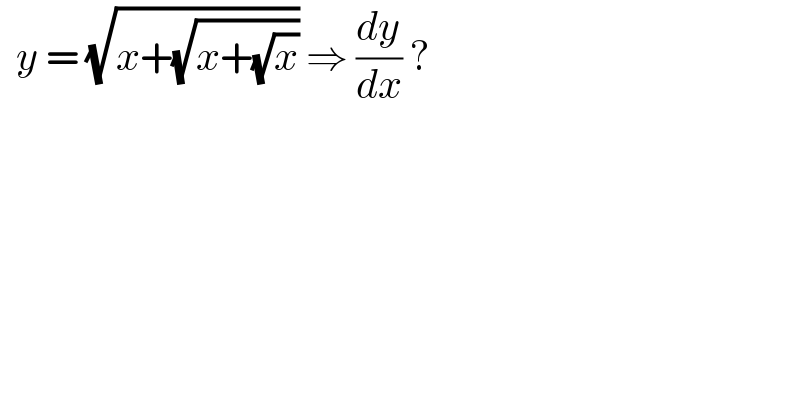
y = (√(x+(√(x+(√x))))) ⇒ (dy/dx) ?
$$\:\:{y}\:=\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}\:\Rightarrow\:\frac{{dy}}{{dx}}\:?\: \\ $$
Answered by ajfour last updated on 25/Aug/20
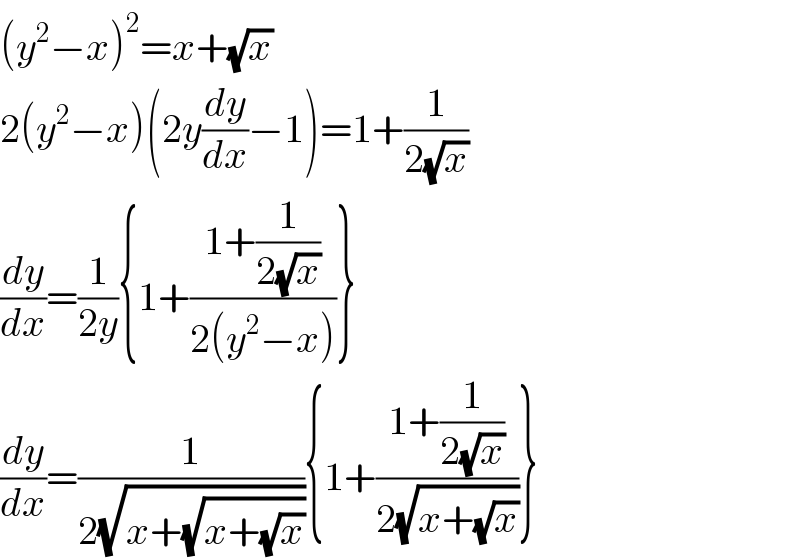
(y^2 −x)^2 =x+(√x) 2(y^2 −x)(2y(dy/dx)−1)=1+(1/(2(√x))) (dy/dx)=(1/(2y)){1+((1+(1/(2(√x))))/(2(y^2 −x)))} (dy/dx)=(1/(2(√(x+(√(x+(√x))))))){1+((1+(1/(2(√x))))/(2(√(x+(√x)))))}
$$\left({y}^{\mathrm{2}} −{x}\right)^{\mathrm{2}} ={x}+\sqrt{{x}} \\ $$$$\mathrm{2}\left({y}^{\mathrm{2}} −{x}\right)\left(\mathrm{2}{y}\frac{{dy}}{{dx}}−\mathrm{1}\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\mathrm{2}{y}}\left\{\mathrm{1}+\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\mathrm{2}\left({y}^{\mathrm{2}} −{x}\right)}\right\} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\sqrt{{x}+\sqrt{{x}}}}}\left\{\mathrm{1}+\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\mathrm{2}\sqrt{{x}+\sqrt{{x}}}}\right\} \\ $$
Answered by bemath last updated on 25/Aug/20
Answered by 1549442205PVT last updated on 25/Aug/20
y=(√(x+(√(x+(√x))))).Squaring two sides we get y^2 =x+(√(x+(√x))) .Derivative two sides by x we get 2y.y′=1+(((x+(√x))′)/(2(√(x+(√x))))) 2y.y′=1+((1+(1/(2(√x))))/(2(√(x+(√x)))))=1+((2(√x)+1)/(4(√x).(√(x+(√x))))) =((4(√(x^2 +x(√x)))+2(√x)+1)/(4(√(x^2 +x(√x))))) ⇒(dy/dx)=((4(√(x^2 +x(√x)))+2(√x)+1)/(4(√(x^2 +x(√x)))))/2y =((4(√(x^2 +x(√x)))+2(√x)+1)/( 2(√(x+(√(x+(√x))).))(4(√(x^2 +x(√x)))))) Check by calculator (d/dx)((√(x+(√(x+(√x))))))∣_(x=1) =0.4924 558242 =((4(√(x^2 +x(√x)))+2(√x)+1)/( 2(√(x+(√(x+(√x))).))(4(√(x^2 +x(√x))))))∣_(x=1)
$$\mathrm{y}=\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}.\mathrm{Squaring}\:\mathrm{two}\:\mathrm{sides}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{y}^{\mathrm{2}} =\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}\:.\mathrm{Derivative}\:\mathrm{two}\:\mathrm{sides} \\ $$$$\mathrm{by}\:\mathrm{x}\:\mathrm{we}\:\mathrm{get}\:\mathrm{2y}.\mathrm{y}'=\mathrm{1}+\frac{\left(\mathrm{x}+\sqrt{\mathrm{x}}\right)'}{\mathrm{2}\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}\: \\ $$$$\mathrm{2y}.\mathrm{y}'=\mathrm{1}+\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}}{\mathrm{2}\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}=\mathrm{1}+\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{x}}.\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}} \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}\sqrt{\mathrm{x}}}+\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}\sqrt{\mathrm{x}}}} \\ $$$$\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{4}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}\sqrt{\mathrm{x}}}+\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}\sqrt{\mathrm{x}}}}/\mathrm{2y} \\ $$$$=\frac{\mathrm{4}\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}\sqrt{\boldsymbol{\mathrm{x}}}}+\mathrm{2}\sqrt{\boldsymbol{\mathrm{x}}}+\mathrm{1}}{\:\mathrm{2}\sqrt{\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}}}.}\left(\mathrm{4}\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}\sqrt{\boldsymbol{\mathrm{x}}}}\right)} \\ $$$$\boldsymbol{\mathrm{Check}}\:\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{calculator}} \\ $$$$\frac{\boldsymbol{\mathrm{d}}}{\boldsymbol{\mathrm{dx}}}\left(\sqrt{\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}}}}\right)\mid_{\boldsymbol{\mathrm{x}}=\mathrm{1}} =\mathrm{0}.\mathrm{4924}\:\mathrm{558242} \\ $$$$=\frac{\mathrm{4}\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}\sqrt{\boldsymbol{\mathrm{x}}}}+\mathrm{2}\sqrt{\boldsymbol{\mathrm{x}}}+\mathrm{1}}{\:\mathrm{2}\sqrt{\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}}}.}\left(\mathrm{4}\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}\sqrt{\boldsymbol{\mathrm{x}}}}\right)}\mid_{\mathrm{x}=\mathrm{1}} \\ $$
Answered by mathmax by abdo last updated on 25/Aug/20
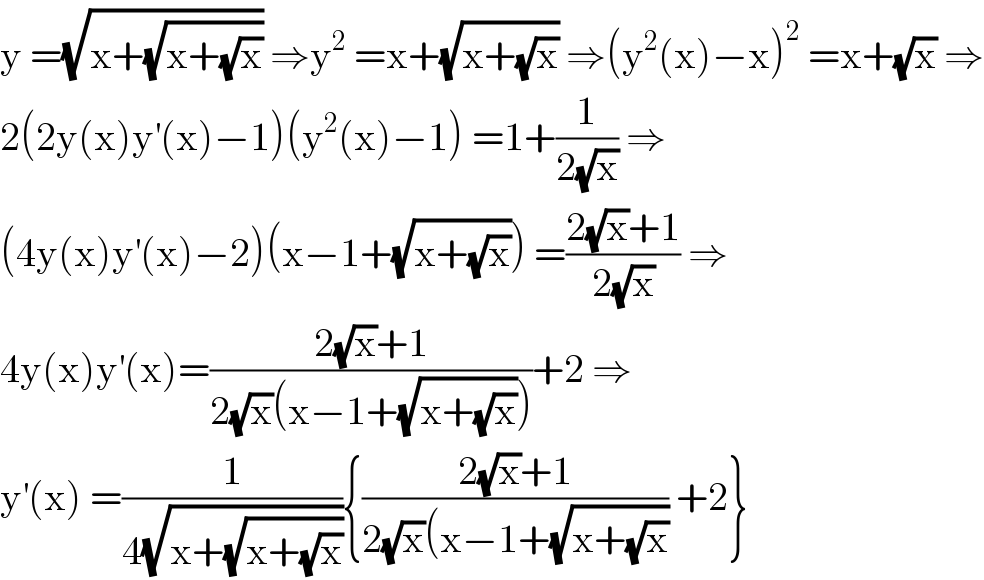
y =(√(x+(√(x+(√x))))) ⇒y^2 =x+(√(x+(√x))) ⇒(y^2 (x)−x)^2 =x+(√x) ⇒ 2(2y(x)y^′ (x)−1)(y^2 (x)−1) =1+(1/(2(√x))) ⇒ (4y(x)y^′ (x)−2)(x−1+(√(x+(√x)))) =((2(√x)+1)/(2(√x))) ⇒ 4y(x)y^′ (x)=((2(√x)+1)/(2(√x)(x−1+(√(x+(√x))))))+2 ⇒ y^′ (x) =(1/(4(√(x+(√(x+(√x))))))){((2(√x)+1)/(2(√x)(x−1+(√(x+(√x))))) +2}
$$\mathrm{y}\:=\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}\:\Rightarrow\mathrm{y}^{\mathrm{2}} \:=\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}\:\Rightarrow\left(\mathrm{y}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{x}\right)^{\mathrm{2}} \:=\mathrm{x}+\sqrt{\mathrm{x}}\:\Rightarrow \\ $$$$\mathrm{2}\left(\mathrm{2y}\left(\mathrm{x}\right)\mathrm{y}^{'} \left(\mathrm{x}\right)−\mathrm{1}\right)\left(\mathrm{y}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{1}\right)\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}\:\Rightarrow \\ $$$$\left(\mathrm{4y}\left(\mathrm{x}\right)\mathrm{y}^{'} \left(\mathrm{x}\right)−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{1}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}\right)\:=\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}\:\Rightarrow \\ $$$$\mathrm{4y}\left(\mathrm{x}\right)\mathrm{y}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}\left(\mathrm{x}−\mathrm{1}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}\right)}+\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{y}^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{x}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}}}\left\{\frac{\mathrm{2}\sqrt{\mathrm{x}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}\left(\mathrm{x}−\mathrm{1}+\sqrt{\mathrm{x}+\sqrt{\mathrm{x}}}\right.}\:+\mathrm{2}\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *