Question Number 62759 by naka3546 last updated on 25/Jun/19

$${y}\:\:=\:\:{x}^{{y}} \\ $$$$\frac{{dy}}{{dx}}\:\:=\:\:? \\ $$
Answered by Kunal12588 last updated on 25/Jun/19
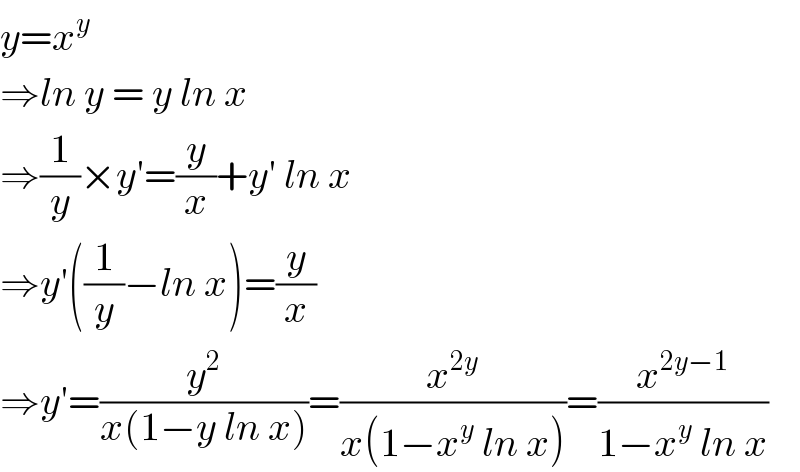
$${y}={x}^{{y}} \\ $$$$\Rightarrow{ln}\:{y}\:=\:{y}\:{ln}\:{x} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{y}}×{y}'=\frac{{y}}{{x}}+{y}'\:{ln}\:{x} \\ $$$$\Rightarrow{y}'\left(\frac{\mathrm{1}}{{y}}−{ln}\:{x}\right)=\frac{{y}}{{x}} \\ $$$$\Rightarrow{y}'=\frac{{y}^{\mathrm{2}} }{{x}\left(\mathrm{1}−{y}\:{ln}\:{x}\right)}=\frac{{x}^{\mathrm{2}{y}} }{{x}\left(\mathrm{1}−{x}^{{y}} \:{ln}\:{x}\right)}=\frac{{x}^{\mathrm{2}{y}−\mathrm{1}} }{\mathrm{1}−{x}^{{y}} \:{ln}\:{x}} \\ $$
