Question Number 49845 by mhozhez last updated on 11/Dec/18
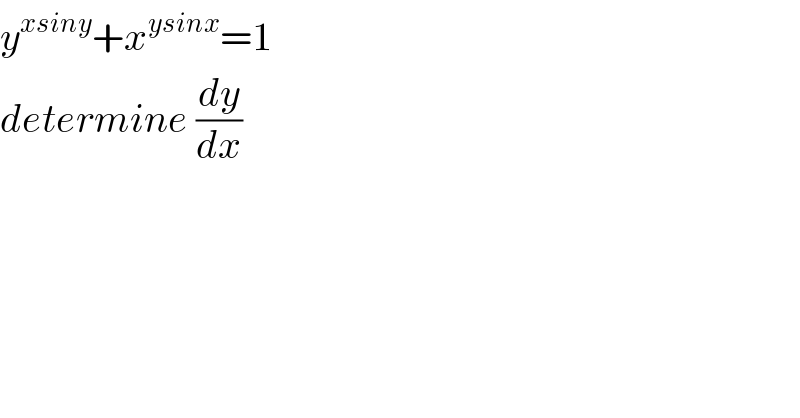
$${y}^{{xsiny}} +{x}^{{ysinx}} =\mathrm{1} \\ $$$${determine}\:\frac{{dy}}{{dx}} \\ $$
Commented by MJS last updated on 11/Dec/18
![try this for yourself. the method is simple: t_i (x,y) are terms in x and y t_1 (x,y)+t_2 (x,y)+...=0 is the same as Σ_(i=1) ^n t_i (x,y)=0 now derivate dxΣ_(i=1) ^n (d/dx)[t_i (x,y)]+dyΣ_(i=1) ^n (d/dy)[t_i (x,y)]=0 ⇒ (dy/dx)=−((Σ_(i=1) ^n (d/dx)[t_i (x,y)])/(Σ_(i=1) ^n (d/dy)[t_i (x,y)])) an example ax^2 +bxy+cy^2 +dx+ey+f=0 dx(2ax+by+0+d+0+0)+dy(0+bx+2cy+0+e+0)=0 dx(2ax+by+d)+dy(bx+2cy+e)=0 (dy/dx)=−((2ax+by+d)/(bx+2cy+e))](https://www.tinkutara.com/question/Q49849.png)
$$\mathrm{try}\:\mathrm{this}\:\mathrm{for}\:\mathrm{yourself}.\:\mathrm{the}\:\mathrm{method}\:\mathrm{is}\:\mathrm{simple}: \\ $$$${t}_{{i}} \left({x},{y}\right)\:\mathrm{are}\:\mathrm{terms}\:\mathrm{in}\:{x}\:\mathrm{and}\:{y} \\ $$$${t}_{\mathrm{1}} \left({x},{y}\right)+{t}_{\mathrm{2}} \left({x},{y}\right)+…=\mathrm{0}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{t}_{{i}} \left({x},{y}\right)=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{derivate} \\ $$$${dx}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{d}}{{dx}}\left[{t}_{{i}} \left({x},{y}\right)\right]+{dy}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{d}}{{dy}}\left[{t}_{{i}} \left({x},{y}\right)\right]=\mathrm{0} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}=−\frac{\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{d}}{{dx}}\left[{t}_{{i}} \left({x},{y}\right)\right]}{\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{d}}{{dy}}\left[{t}_{{i}} \left({x},{y}\right)\right]} \\ $$$$\mathrm{an}\:\mathrm{example} \\ $$$${ax}^{\mathrm{2}} +{bxy}+{cy}^{\mathrm{2}} +{dx}+{ey}+{f}=\mathrm{0} \\ $$$${dx}\left(\mathrm{2}{ax}+{by}+\mathrm{0}+{d}+\mathrm{0}+\mathrm{0}\right)+{dy}\left(\mathrm{0}+{bx}+\mathrm{2}{cy}+\mathrm{0}+{e}+\mathrm{0}\right)=\mathrm{0} \\ $$$${dx}\left(\mathrm{2}{ax}+{by}+{d}\right)+{dy}\left({bx}+\mathrm{2}{cy}+{e}\right)=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=−\frac{\mathrm{2}{ax}+{by}+{d}}{{bx}+\mathrm{2}{cy}+{e}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Dec/18
![u=y^(xsiny) lnu=xsinylny (1/u)×(du/dx)=xsiny×(1/y)(dy/dx)+xlny×cosy×(dy/dx)+sinylny (du/dx)=y^(xsiny) [(dy/dx)(((xsiny)/y)+xcosylny)+sinylny] v=x^(ysinx) lnv=ysinxlnx (1/v)(dv/dx)=((ysinx)/x)+ylnxcosx+sinxlnx(dy/dx) (dv/dx)=x^(ysinx) (((ysinx)/x)+ylnxcosx+sinxlnx(dy/dx)) u+v=1 (du/dx)+(dv/dx)=0 y^(xsiny) [(dy/dx)(((xsiny)/y)+xcosylny)+sinylny]+x^(ysinx) [((ysinx)/x)+ylnxcosx+sinxlnx(dy/dx)]=0 (dy/dx)[y^(xsiny) (((xsiny)/y)+xcosylny)+(x^(ysinx) sinxlnx)]=−[x^(ysinx) (((ysinx)/x)+ylnxcosx)+y^(xsiny) (sinylny)] (dy/dx)=((−[x^(ysinx) (((ysinx)/x)+ylnxcosx)+y^(xsiny) (sinylny)])/([y^(xsiny) (((xsiny)/y)+xcosylny)+(x^(ysinx) sinxlnx)])) it is the answer...](https://www.tinkutara.com/question/Q49847.png)
$${u}={y}^{{xsiny}} \\ $$$${lnu}={xsinylny} \\ $$$$\frac{\mathrm{1}}{{u}}×\frac{{du}}{{dx}}={xsiny}×\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dx}}+{xlny}×{cosy}×\frac{{dy}}{{dx}}+{sinylny} \\ $$$$\frac{{du}}{{dx}}={y}^{{xsiny}} \left[\frac{{dy}}{{dx}}\left(\frac{{xsiny}}{{y}}+{xcosylny}\right)+{sinylny}\right] \\ $$$${v}={x}^{{ysinx}} \\ $$$${lnv}={ysinxlnx} \\ $$$$\frac{\mathrm{1}}{{v}}\frac{{dv}}{{dx}}=\frac{{ysinx}}{{x}}+{ylnxcosx}+{sinxlnx}\frac{{dy}}{{dx}} \\ $$$$\frac{{dv}}{{dx}}={x}^{{ysinx}} \left(\frac{{ysinx}}{{x}}+{ylnxcosx}+{sinxlnx}\frac{{dy}}{{dx}}\right) \\ $$$${u}+{v}=\mathrm{1} \\ $$$$\frac{{du}}{{dx}}+\frac{{dv}}{{dx}}=\mathrm{0} \\ $$$${y}^{{xsiny}} \left[\frac{{dy}}{{dx}}\left(\frac{{xsiny}}{{y}}+{xcosylny}\right)+{sinylny}\right]+{x}^{{ysinx}} \left[\frac{{ysinx}}{{x}}+{ylnxcosx}+{sinxlnx}\frac{{dy}}{{dx}}\right]=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}\left[{y}^{{xsiny}} \left(\frac{{xsiny}}{{y}}+{xcosylny}\right)+\left({x}^{{ysinx}} {sinxlnx}\right)\right]=−\left[{x}^{{ysinx}} \left(\frac{{ysinx}}{{x}}+{ylnxcosx}\right)+{y}^{{xsiny}} \left({sinylny}\right)\right] \\ $$$$\frac{{dy}}{{dx}}=\frac{−\left[{x}^{{ysinx}} \left(\frac{{ysinx}}{{x}}+{ylnxcosx}\right)+{y}^{{xsiny}} \left({sinylny}\right)\right]}{\left[{y}^{{xsiny}} \left(\frac{{xsiny}}{{y}}+{xcosylny}\right)+\left({x}^{{ysinx}} {sinxlnx}\right)\right]} \\ $$$${it}\:{is}\:{the}\:{answer}… \\ $$
