Question Number 94328 by i jagooll last updated on 18/May/20

$$\mathrm{y}'\:+\:\mathrm{xy}\:=\:\mathrm{x}\: \\ $$
Answered by i jagooll last updated on 18/May/20
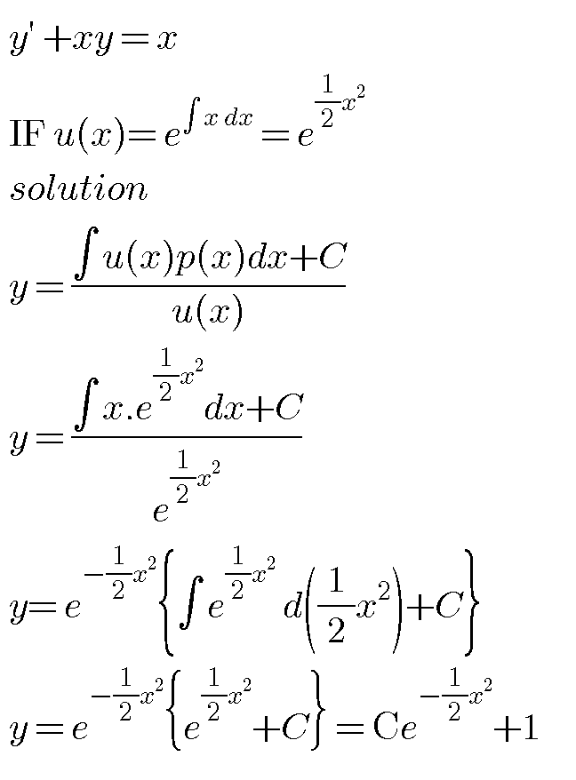
Commented by i jagooll last updated on 18/May/20

$$\mathrm{it}\:\mathrm{correct}\:? \\ $$
Answered by abdomathmax last updated on 18/May/20
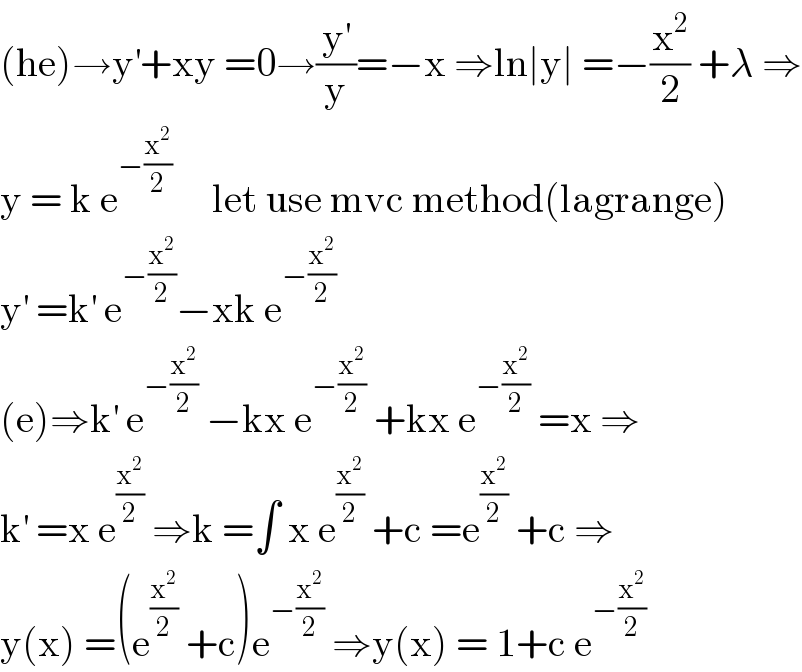
$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{'} +\mathrm{xy}\:=\mathrm{0}\rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}=−\mathrm{x}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\lambda\:\Rightarrow \\ $$$$\mathrm{y}\:=\:\mathrm{k}\:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:\:\:\:\mathrm{let}\:\mathrm{use}\:\mathrm{mvc}\:\mathrm{method}\left(\mathrm{lagrange}\right) \\ $$$$\mathrm{y}^{'} \:=\mathrm{k}^{'} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} −\mathrm{xk}\:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{k}^{'} \:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:−\mathrm{kx}\:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:+\mathrm{kx}\:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:=\mathrm{x}\:\Rightarrow \\ $$$$\mathrm{k}^{'} \:=\mathrm{x}\:\mathrm{e}^{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\Rightarrow\mathrm{k}\:=\int\:\mathrm{x}\:\mathrm{e}^{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:+\mathrm{c}\:=\mathrm{e}^{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\left(\mathrm{e}^{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:+\mathrm{c}\right)\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\:\mathrm{1}+\mathrm{c}\:\mathrm{e}^{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$
