Question Number 157033 by amin96 last updated on 18/Oct/21
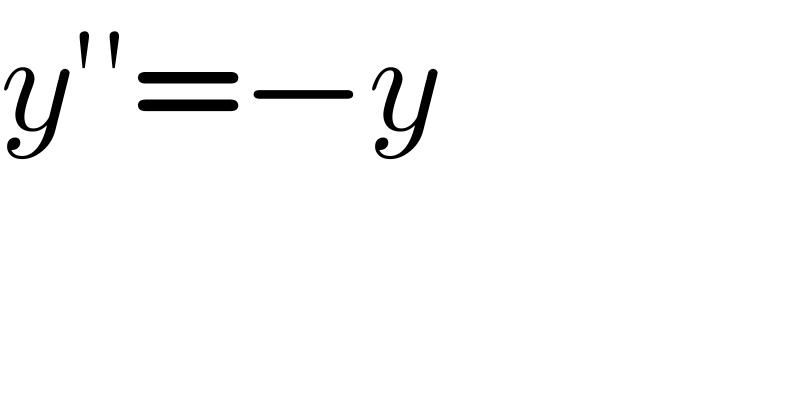
$${y}''=−{y} \\ $$
Commented by aliyn last updated on 19/Oct/21
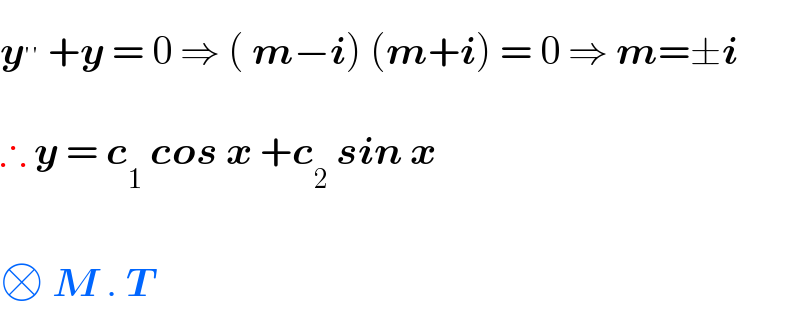
$$\boldsymbol{{y}}^{''} \:+\boldsymbol{{y}}\:=\:\mathrm{0}\:\Rightarrow\:\left(\:\boldsymbol{{m}}−\boldsymbol{{i}}\right)\:\left(\boldsymbol{{m}}+\boldsymbol{{i}}\right)\:=\:\mathrm{0}\:\Rightarrow\:\boldsymbol{{m}}=\pm\boldsymbol{{i}} \\ $$$$ \\ $$$$\therefore\:\boldsymbol{{y}}\:=\:\boldsymbol{{c}}_{\mathrm{1}} \:\boldsymbol{{cos}}\:\boldsymbol{{x}}\:+\boldsymbol{{c}}_{\mathrm{2}} \:\boldsymbol{{sin}}\:\boldsymbol{{x}} \\ $$$$ \\ $$$$\square\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}} \\ $$
Answered by puissant last updated on 18/Oct/21
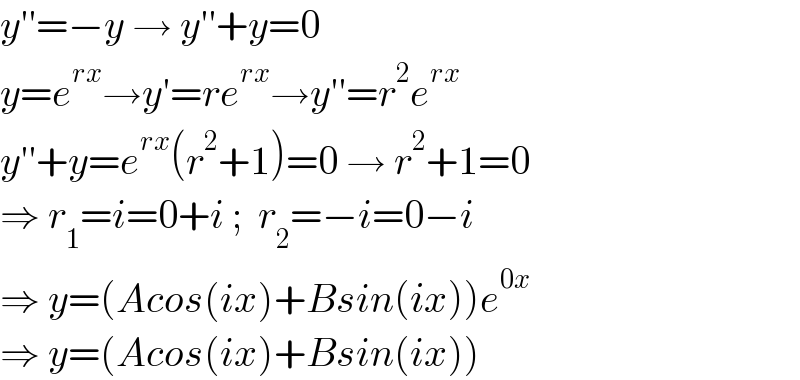
$${y}''=−{y}\:\rightarrow\:{y}''+{y}=\mathrm{0}\: \\ $$$${y}={e}^{{rx}} \rightarrow{y}'={re}^{{rx}} \rightarrow{y}''={r}^{\mathrm{2}} {e}^{{rx}} \\ $$$${y}''+{y}={e}^{{rx}} \left({r}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0}\:\rightarrow\:{r}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{r}_{\mathrm{1}} ={i}=\mathrm{0}+{i}\:;\:\:{r}_{\mathrm{2}} =−{i}=\mathrm{0}−{i} \\ $$$$\Rightarrow\:{y}=\left({Acos}\left({ix}\right)+{Bsin}\left({ix}\right)\right){e}^{\mathrm{0}{x}} \\ $$$$\Rightarrow\:{y}=\left({Acos}\left({ix}\right)+{Bsin}\left({ix}\right)\right) \\ $$
Answered by amin96 last updated on 18/Oct/21
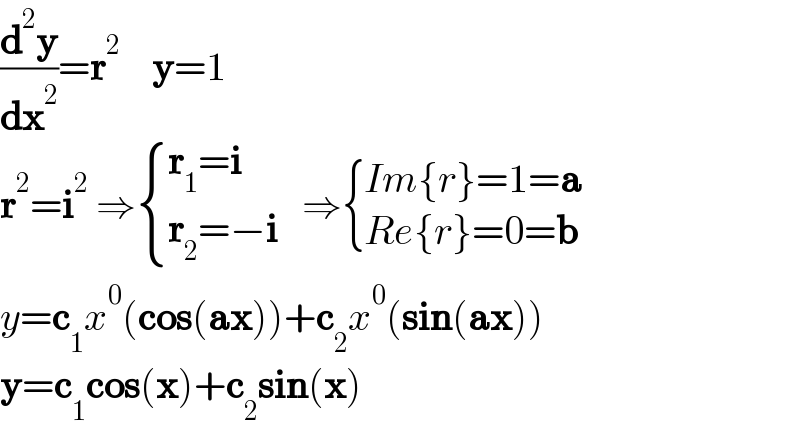
$$\frac{\boldsymbol{\mathrm{d}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{2}} }=\boldsymbol{\mathrm{r}}^{\mathrm{2}} \:\:\:\:\boldsymbol{\mathrm{y}}=\mathrm{1} \\ $$$$\boldsymbol{\mathrm{r}}^{\mathrm{2}} =\boldsymbol{\mathrm{i}}^{\mathrm{2}} \:\Rightarrow\begin{cases}{\boldsymbol{\mathrm{r}}_{\mathrm{1}} =\boldsymbol{\mathrm{i}}}\\{\boldsymbol{\mathrm{r}}_{\mathrm{2}} =−\boldsymbol{\mathrm{i}}}\end{cases}\:\:\:\Rightarrow\begin{cases}{{Im}\left\{{r}\right\}=\mathrm{1}=\boldsymbol{\mathrm{a}}}\\{{Re}\left\{{r}\right\}=\mathrm{0}=\boldsymbol{\mathrm{b}}}\end{cases} \\ $$$${y}=\boldsymbol{\mathrm{c}}_{\mathrm{1}} {x}^{\mathrm{0}} \left(\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{ax}}\right)\right)+\boldsymbol{\mathrm{c}}_{\mathrm{2}} {x}^{\mathrm{0}} \left(\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{ax}}\right)\right) \\ $$$$\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{c}}_{\mathrm{1}} \boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{c}}_{\mathrm{2}} \boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{x}}\right) \\ $$
Answered by mr W last updated on 18/Oct/21
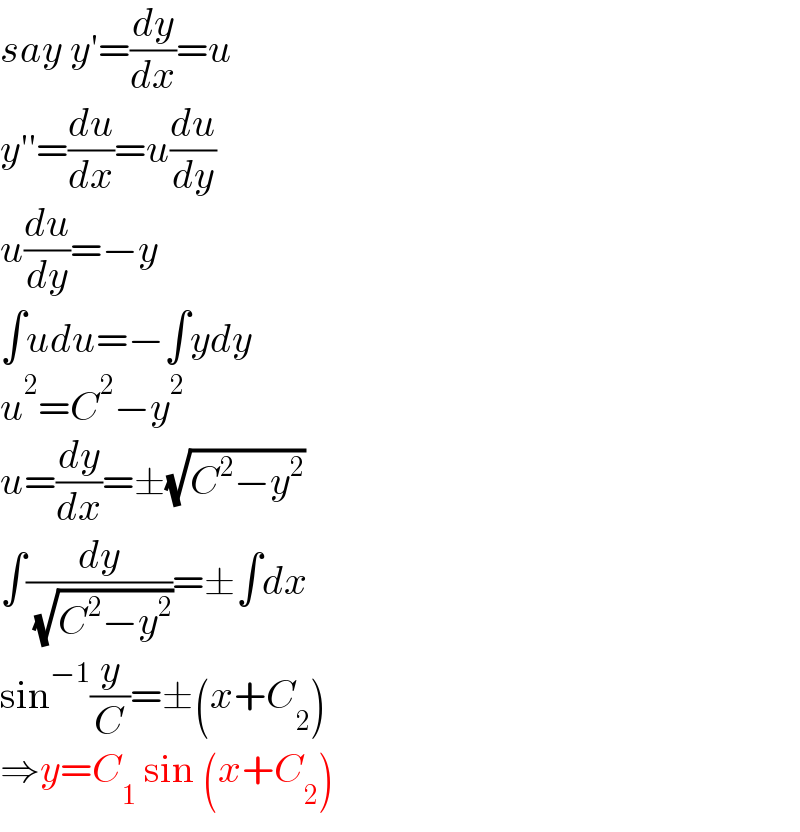
$${say}\:{y}'=\frac{{dy}}{{dx}}={u} \\ $$$${y}''=\frac{{du}}{{dx}}={u}\frac{{du}}{{dy}} \\ $$$${u}\frac{{du}}{{dy}}=−{y} \\ $$$$\int{udu}=−\int{ydy} \\ $$$${u}^{\mathrm{2}} ={C}^{\mathrm{2}} −{y}^{\mathrm{2}} \\ $$$${u}=\frac{{dy}}{{dx}}=\pm\sqrt{{C}^{\mathrm{2}} −{y}^{\mathrm{2}} } \\ $$$$\int\frac{{dy}}{\:\sqrt{{C}^{\mathrm{2}} −{y}^{\mathrm{2}} }}=\pm\int{dx} \\ $$$$\mathrm{sin}^{−\mathrm{1}} \frac{{y}}{{C}}=\pm\left({x}+{C}_{\mathrm{2}} \right) \\ $$$$\Rightarrow{y}={C}_{\mathrm{1}} \:\mathrm{sin}\:\left({x}+{C}_{\mathrm{2}} \right) \\ $$
