Menu Close

y-y-3y-2x-

Tinku Tara 0 Comments
Pin




Question Number 126122 by benjo_mathlover last updated on 17/Dec/20
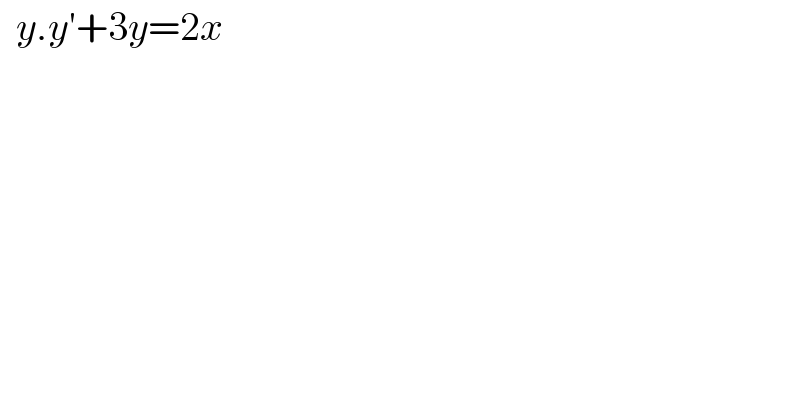
y.y′+3y=2x
$$\:\:{y}.{y}'+\mathrm{3}{y}=\mathrm{2}{x}\: \\ $$
Answered by Dwaipayan Shikari last updated on 17/Dec/20
y′+3=((2x)/y) y=vx⇒y′=v+xv′ ⇒xv′+v+3=(2/v)⇒xv′=((2−v^2 −3v)/v) ⇒∫(v/(v^2 +3v−2))dv=−∫(dx/x) ⇒(1/2)∫((2v+3)/(v^2 −3v+2))dv−(3/2)∫(dv/((v+(3/2))^2 −(((√(17))/2))^2 ))=log((C/x)) ⇒(1/2)log(v^2 −3v+2)+(3/(2(√(17))))log(((v+((3+(√(17)))/2))/(v+((3−(√(17)))/2))))=log((C/x)) ((y^2 /x^2 )−3(y/x)+2)((((2y+3x+x(√(17)))/(2y+3x−x(√(17))))))^(3/( (√(17)))) =(C^2 /x^2 )
$${y}'+\mathrm{3}=\frac{\mathrm{2}{x}}{{y}}\:\:\:\:\:\:\:\:{y}={vx}\Rightarrow{y}'={v}+{xv}' \\ $$$$\Rightarrow{xv}'+{v}+\mathrm{3}=\frac{\mathrm{2}}{{v}}\Rightarrow{xv}'=\frac{\mathrm{2}−{v}^{\mathrm{2}} −\mathrm{3}{v}}{{v}} \\ $$$$\Rightarrow\int\frac{{v}}{{v}^{\mathrm{2}} +\mathrm{3}{v}−\mathrm{2}}{dv}=−\int\frac{{dx}}{{x}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{v}+\mathrm{3}}{{v}^{\mathrm{2}} −\mathrm{3}{v}+\mathrm{2}}{dv}−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dv}}{\left({v}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{17}}}{\mathrm{2}}\right)^{\mathrm{2}} }={log}\left(\frac{{C}}{{x}}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}{log}\left({v}^{\mathrm{2}} −\mathrm{3}{v}+\mathrm{2}\right)+\frac{\mathrm{3}}{\mathrm{2}\sqrt{\mathrm{17}}}{log}\left(\frac{{v}+\frac{\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}}{{v}+\frac{\mathrm{3}−\sqrt{\mathrm{17}}}{\mathrm{2}}}\right)={log}\left(\frac{{C}}{{x}}\right) \\ $$$$\left(\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }−\mathrm{3}\frac{{y}}{{x}}+\mathrm{2}\right)\left(\left(\frac{\mathrm{2}{y}+\mathrm{3}{x}+{x}\sqrt{\mathrm{17}}}{\mathrm{2}{y}+\mathrm{3}{x}−{x}\sqrt{\mathrm{17}}}\right)\right)^{\frac{\mathrm{3}}{\:\sqrt{\mathrm{17}}}} =\frac{{C}^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$
Answered by liberty last updated on 17/Dec/20
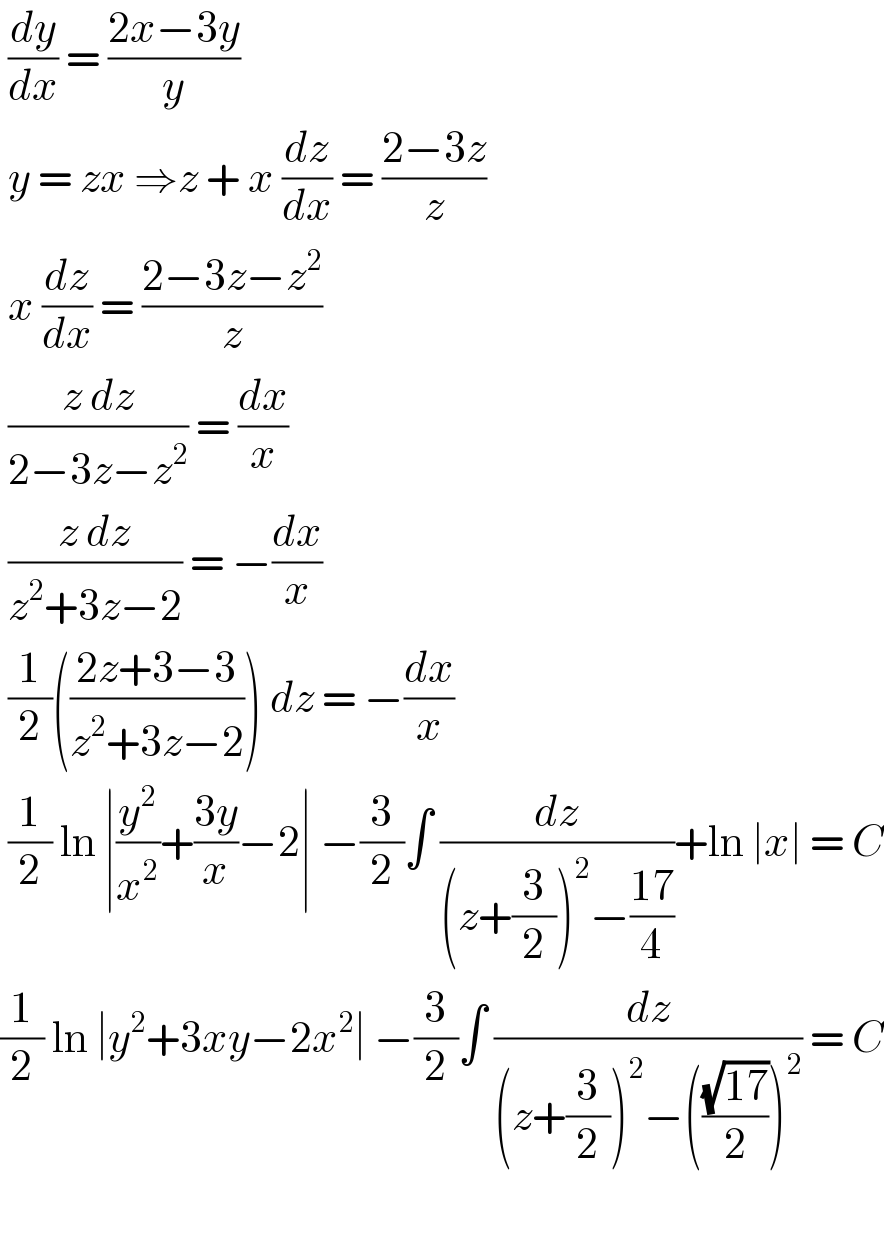
(dy/dx) = ((2x−3y)/y) y = zx ⇒z + x (dz/dx) = ((2−3z)/z) x (dz/dx) = ((2−3z−z^2 )/z) ((z dz)/(2−3z−z^2 )) = (dx/x) ((z dz)/(z^2 +3z−2)) = −(dx/x) (1/2)(((2z+3−3)/(z^2 +3z−2))) dz = −(dx/x) (1/2) ln ∣(y^2 /x^2 )+((3y)/x)−2∣ −(3/2)∫ (dz/((z+(3/2))^2 −((17)/4)))+ln ∣x∣ = C (1/2) ln ∣y^2 +3xy−2x^2 ∣ −(3/2)∫ (dz/((z+(3/2))^2 −(((√(17))/2))^2 )) = C
$$\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{2}{x}−\mathrm{3}{y}}{{y}} \\ $$$$\:{y}\:=\:{zx}\:\Rightarrow{z}\:+\:{x}\:\frac{{dz}}{{dx}}\:=\:\frac{\mathrm{2}−\mathrm{3}{z}}{{z}} \\ $$$$\:{x}\:\frac{{dz}}{{dx}}\:=\:\frac{\mathrm{2}−\mathrm{3}{z}−{z}^{\mathrm{2}} }{{z}} \\ $$$$\:\frac{{z}\:{dz}}{\mathrm{2}−\mathrm{3}{z}−{z}^{\mathrm{2}} }\:=\:\frac{{dx}}{{x}} \\ $$$$\:\frac{{z}\:{dz}}{{z}^{\mathrm{2}} +\mathrm{3}{z}−\mathrm{2}}\:=\:−\frac{{dx}}{{x}} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}{z}+\mathrm{3}−\mathrm{3}}{{z}^{\mathrm{2}} +\mathrm{3}{z}−\mathrm{2}}\right)\:{dz}\:=\:−\frac{{dx}}{{x}} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\mid\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }+\frac{\mathrm{3}{y}}{{x}}−\mathrm{2}\mid\:−\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{{dz}}{\left({z}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{17}}{\mathrm{4}}}+\mathrm{ln}\:\mid{x}\mid\:=\:{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\mid{y}^{\mathrm{2}} +\mathrm{3}{xy}−\mathrm{2}{x}^{\mathrm{2}} \mid\:−\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{{dz}}{\left({z}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{17}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:=\:{C} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *