Menu Close

y-y-6y-x-

Tinku Tara 0 Comments
Pin




Question Number 105879 by john santu last updated on 01/Aug/20
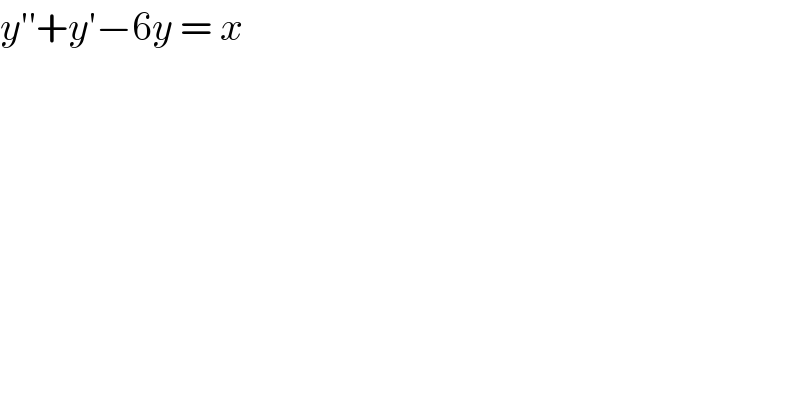
y′′+y′−6y = x
$${y}''+{y}'−\mathrm{6}{y}\:=\:{x}\: \\ $$
Answered by bemath last updated on 01/Aug/20
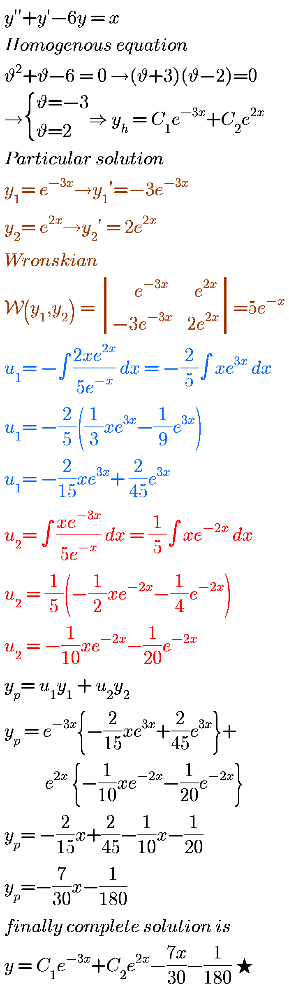
Answered by mathmax by abdo last updated on 01/Aug/20
y^(′′) +y^′ −6y =x h→y^(′′) +y^′ −6y =0→r^2 +r−6 =0→Δ =1+24=25 ⇒ r_1 =((−1+5)/2) =2 and r_2 =((−1−5)/2) =−3 ⇒y_h =ae^(2x) +be^(−3x) =au_1 +bu_2 W(u_1 ,u_2 ) = determinant (((e^(2x) e^(−3x) )),((2e^(2x) −3e^(−3x) )))=−3e^(−x) −2e^(−x) =−5e^(−x) ≠0 W_1 = determinant (((o e^(−3x) )),((x −3e^(−3x) )))=−xe^(−3x) W_2 = determinant (((e^(2x) 0)),((2e^(2x) x)))=xe^(2x) ⇒ v_1 =∫ (w_1 /w)dx =∫ ((−xe^(−3x) )/(−5e^(−x) ))dx =(1/5)∫x e^(−2x) dx ⇒5v_1 =−(x/2)e^(−2x) +∫ (1/2)e^(−2x) dx =−(x/2)e^(−2x) −(1/4)e^(−2x) =−((x/2)+(1/4))e^(−2x) ⇒v_1 =−((x/(10)) +(1/(2o)))e^(−2x) v_2 =∫ (w_2 /w)dx =∫ ((xe^(2x) )/(−5e^(−x) ))dx =−(1/5) ∫ xe^(3x) dx =−(1/5){ (x/3)e^(3x) −∫ (1/3)e^(3x) dx} =−(1/5){(x/3)e^(3x) −(1/9)e^(3x) } ={(1/(45))−(x/(15))}e^(3x) ⇒y_p =u_1 v_(1 ) +u_2 v_2 =−e^(2x) ×((x/(10)) +(1/(20)))e^(−2x) + e^(−3x) ×{(1/(45))−(x/(15))}e^(3x) =−(x/(10))−(1/(20)) +(1/(45))−(x/(15)) =−((1/(10))+(1/(15)))x +(1/(45))−(1/(20)) =−((25)/(150)) x −((25)/(900))(rest simplification!) the general solution is y =ae^(2x) +b e^(−3x) −((25)/(150))x−((25)/(900))
$$\mathrm{y}^{''} \:+\mathrm{y}^{'} −\mathrm{6y}\:=\mathrm{x} \\ $$$$\mathrm{h}\rightarrow\mathrm{y}^{''} \:+\mathrm{y}^{'} −\mathrm{6y}\:=\mathrm{0}\rightarrow\mathrm{r}^{\mathrm{2}} +\mathrm{r}−\mathrm{6}\:=\mathrm{0}\rightarrow\Delta\:=\mathrm{1}+\mathrm{24}=\mathrm{25}\:\Rightarrow \\ $$$$\mathrm{r}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{5}}{\mathrm{2}}\:=\mathrm{2}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{5}}{\mathrm{2}}\:=−\mathrm{3}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\mathrm{2x}} \:+\mathrm{be}^{−\mathrm{3x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{3x}} }\\{\mathrm{2e}^{\mathrm{2x}} \:\:\:\:\:\:\:\:−\mathrm{3e}^{−\mathrm{3x}} }\end{vmatrix}=−\mathrm{3e}^{−\mathrm{x}} −\mathrm{2e}^{−\mathrm{x}} \:=−\mathrm{5e}^{−\mathrm{x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{3x}} }\\{\mathrm{x}\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3e}^{−\mathrm{3x}} }\end{vmatrix}=−\mathrm{xe}^{−\mathrm{3x}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{2e}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:\mathrm{x}}\end{vmatrix}=\mathrm{xe}^{\mathrm{2x}} \:\:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\:\frac{−\mathrm{xe}^{−\mathrm{3x}} }{−\mathrm{5e}^{−\mathrm{x}} }\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{5}}\int\mathrm{x}\:\mathrm{e}^{−\mathrm{2x}} \mathrm{dx} \\ $$$$\Rightarrow\mathrm{5v}_{\mathrm{1}} =−\frac{\mathrm{x}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} +\int\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} \mathrm{dx}\:=−\frac{\mathrm{x}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} −\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{2x}} \\ $$$$=−\left(\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\mathrm{e}^{−\mathrm{2x}} \:\Rightarrow\mathrm{v}_{\mathrm{1}} =−\left(\frac{\mathrm{x}}{\mathrm{10}}\:+\frac{\mathrm{1}}{\mathrm{2o}}\right)\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{xe}^{\mathrm{2x}} }{−\mathrm{5e}^{−\mathrm{x}} }\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{5}}\:\int\:\mathrm{xe}^{\mathrm{3x}} \mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}}\left\{\:\frac{\mathrm{x}}{\mathrm{3}}\mathrm{e}^{\mathrm{3x}} −\int\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{3x}} \mathrm{dx}\right\}\:=−\frac{\mathrm{1}}{\mathrm{5}}\left\{\frac{\mathrm{x}}{\mathrm{3}}\mathrm{e}^{\mathrm{3x}} −\frac{\mathrm{1}}{\mathrm{9}}\mathrm{e}^{\mathrm{3x}} \right\} \\ $$$$=\left\{\frac{\mathrm{1}}{\mathrm{45}}−\frac{\mathrm{x}}{\mathrm{15}}\right\}\mathrm{e}^{\mathrm{3x}} \:\:\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}\:} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \\ $$$$=−\mathrm{e}^{\mathrm{2x}} ×\left(\frac{\mathrm{x}}{\mathrm{10}}\:+\frac{\mathrm{1}}{\mathrm{20}}\right)\mathrm{e}^{−\mathrm{2x}} \:+\:\mathrm{e}^{−\mathrm{3x}} ×\left\{\frac{\mathrm{1}}{\mathrm{45}}−\frac{\mathrm{x}}{\mathrm{15}}\right\}\mathrm{e}^{\mathrm{3x}} \\ $$$$=−\frac{\mathrm{x}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{20}}\:+\frac{\mathrm{1}}{\mathrm{45}}−\frac{\mathrm{x}}{\mathrm{15}}\:=−\left(\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{15}}\right)\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{45}}−\frac{\mathrm{1}}{\mathrm{20}} \\ $$$$=−\frac{\mathrm{25}}{\mathrm{150}}\:\mathrm{x}\:\:−\frac{\mathrm{25}}{\mathrm{900}}\left(\mathrm{rest}\:\mathrm{simplification}!\right) \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{ae}^{\mathrm{2x}} \:+\mathrm{b}\:\mathrm{e}^{−\mathrm{3x}} −\frac{\mathrm{25}}{\mathrm{150}}\mathrm{x}−\frac{\mathrm{25}}{\mathrm{900}} \\ $$$$ \\ $$$$ \\ $$
Commented by Coronavirus last updated on 01/Aug/20
Intéressant
Answered by john santu last updated on 01/Aug/20
particular solution y_p = Ax^2 +Bx+C y′=2Ax+B ⇒y′′=2A comparing coefficient 2A+2Ax+B−6Ax^2 −6Bx−6C=x −6Ax^2 +(2A−6B)x+2A+B−6C=x { ((A=0)),((2A−6B=1→B=−(1/6))),((2A+B−6C=0→C=−(1/(36)))) :} y_p = −(1/6)x−(1/(36)) ■
$${particular}\:{solution} \\ $$$${y}_{{p}} \:=\:{Ax}^{\mathrm{2}} +{Bx}+{C}\: \\ $$$${y}'=\mathrm{2}{Ax}+{B}\:\Rightarrow{y}''=\mathrm{2}{A} \\ $$$${comparing}\:{coefficient}\: \\ $$$$\mathrm{2}{A}+\mathrm{2}{Ax}+{B}−\mathrm{6}{Ax}^{\mathrm{2}} −\mathrm{6}{Bx}−\mathrm{6}{C}={x} \\ $$$$−\mathrm{6}{Ax}^{\mathrm{2}} +\left(\mathrm{2}{A}−\mathrm{6}{B}\right){x}+\mathrm{2}{A}+{B}−\mathrm{6}{C}={x} \\ $$$$\begin{cases}{{A}=\mathrm{0}}\\{\mathrm{2}{A}−\mathrm{6}{B}=\mathrm{1}\rightarrow{B}=−\frac{\mathrm{1}}{\mathrm{6}}}\\{\mathrm{2}{A}+{B}−\mathrm{6}{C}=\mathrm{0}\rightarrow{C}=−\frac{\mathrm{1}}{\mathrm{36}}}\end{cases} \\ $$$${y}_{{p}} \:=\:−\frac{\mathrm{1}}{\mathrm{6}}{x}−\frac{\mathrm{1}}{\mathrm{36}}\:\blacksquare\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *