Question Number 167930 by mkam last updated on 29/Mar/22
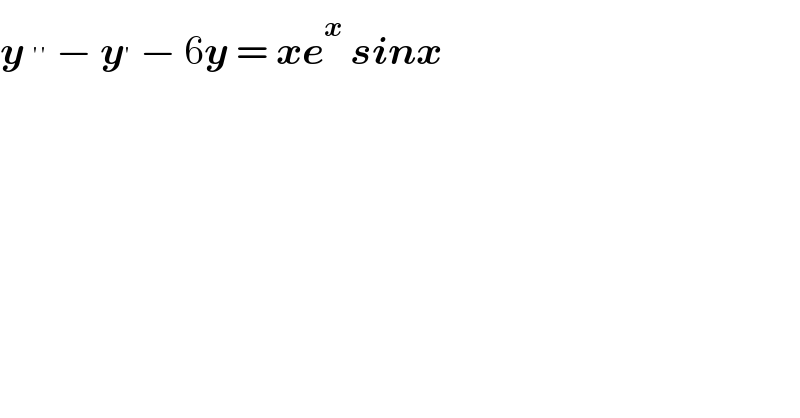
$$\boldsymbol{{y}}\:^{''} \:−\:\boldsymbol{{y}}^{'} \:−\:\mathrm{6}\boldsymbol{{y}}\:=\:\boldsymbol{{xe}}^{\boldsymbol{{x}}} \:\boldsymbol{{sinx}} \\ $$
Commented by mokys last updated on 29/Mar/22

$$???? \\ $$
Answered by qaz last updated on 30/Mar/22

$$\mathrm{y}_{\mathrm{p}} =\frac{\mathrm{1}}{\left(\mathrm{D}−\mathrm{3}\right)\left(\mathrm{D}+\mathrm{2}\right)}\mathrm{xe}^{\mathrm{x}} \mathrm{sin}\:\mathrm{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{e}^{\mathrm{x}} \Im\left(\frac{\mathrm{1}}{\mathrm{D}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{D}+\mathrm{3}}\right)\mathrm{xe}^{\mathrm{ix}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{e}^{\mathrm{x}} \Im\mathrm{e}^{\mathrm{ix}} \left(\frac{\mathrm{1}}{\mathrm{D}−\mathrm{2}+\mathrm{i}}−\frac{\mathrm{1}}{\mathrm{D}+\mathrm{3}+\mathrm{i}}\right)\mathrm{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{e}^{\mathrm{x}} \Im\mathrm{e}^{\mathrm{ix}} \left(−\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{i}\right)\left(\mathrm{1}−\frac{\mathrm{D}}{\mathrm{2}−\mathrm{i}}\right)}−\frac{\mathrm{1}}{\left(\mathrm{3}+\mathrm{i}\right)\left(\mathrm{1}+\frac{\mathrm{D}}{\mathrm{3}+\mathrm{i}}\right)}\right)\mathrm{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{e}^{\mathrm{x}} \Im\mathrm{e}^{\mathrm{ix}} \left(−\frac{\mathrm{1}}{\mathrm{2}−\mathrm{i}}\left(\mathrm{1}+\frac{\mathrm{D}}{\mathrm{2}−\mathrm{i}}+…\right)−\frac{\mathrm{1}}{\mathrm{3}+\mathrm{i}}\left(\mathrm{1}−\frac{\mathrm{D}}{\mathrm{3}+\mathrm{i}}+…\right)\right)\mathrm{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{e}^{\mathrm{x}} \Im\mathrm{e}^{\mathrm{ix}} \left(−\frac{\mathrm{1}}{\mathrm{2}−\mathrm{i}}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}−\mathrm{i}}\right)−\frac{\mathrm{1}}{\mathrm{3}+\mathrm{i}}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{3}+\mathrm{i}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{e}^{\mathrm{x}} \Im\mathrm{e}^{\mathrm{ix}} \left(−\frac{\mathrm{7}}{\mathrm{10}}\mathrm{x}−\frac{\mathrm{i}}{\mathrm{10}}\mathrm{x}−\frac{\mathrm{1}}{\mathrm{25}}−\frac{\mathrm{11}}{\mathrm{50}}\mathrm{i}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{e}^{\mathrm{x}} \left(\left(\frac{\mathrm{7}}{\mathrm{10}}\mathrm{x}+\frac{\mathrm{1}}{\mathrm{25}}\right)\mathrm{sin}\:\mathrm{x}+\left(\frac{\mathrm{1}}{\mathrm{10}}\mathrm{x}+\frac{\mathrm{11}}{\mathrm{50}}\right)\mathrm{cos}\:\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{y}=\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{3x}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{−\mathrm{2x}} −\frac{\mathrm{1}}{\mathrm{5}}\mathrm{e}^{\mathrm{x}} \left(\left(\frac{\mathrm{7}}{\mathrm{10}}\mathrm{x}+\frac{\mathrm{1}}{\mathrm{25}}\right)\mathrm{sin}\:\mathrm{x}+\left(\frac{\mathrm{1}}{\mathrm{10}}\mathrm{x}+\frac{\mathrm{11}}{\mathrm{50}}\right)\mathrm{cos}\:\mathrm{x}\right) \\ $$
