Question Number 154846 by SANOGO last updated on 22/Sep/21
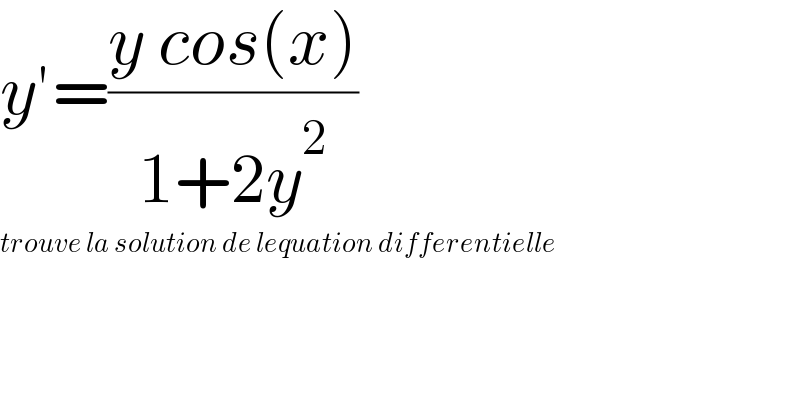
$${y}'=\frac{{y}\:{cos}\left({x}\right)}{\mathrm{1}+\mathrm{2}{y}^{\mathrm{2}} } \\ $$$${trouve}\:{la}\:{solution}\:{de}\:{lequation}\:{differentielle} \\ $$
Commented by tabata last updated on 22/Sep/21
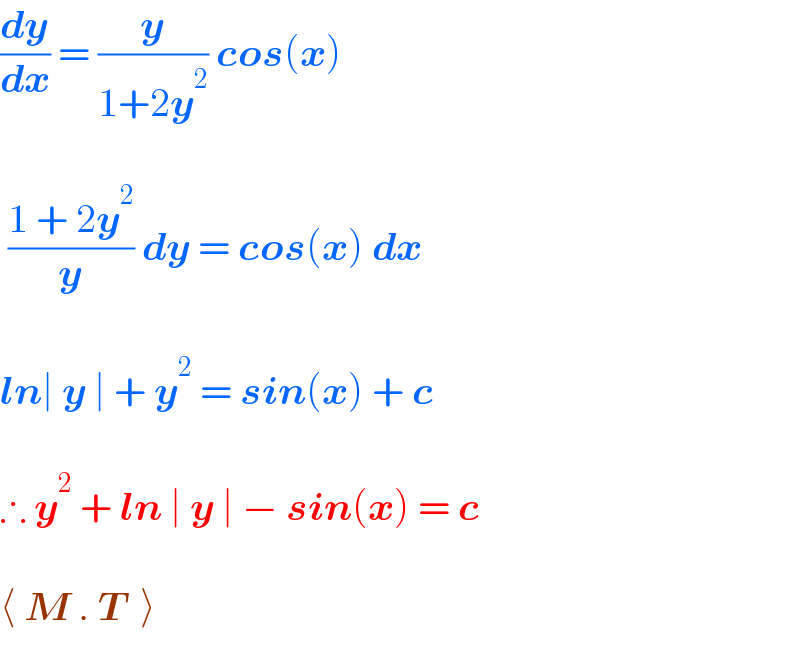
$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}\:=\:\frac{\boldsymbol{{y}}}{\mathrm{1}+\mathrm{2}\boldsymbol{{y}}^{\mathrm{2}} }\:\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)\: \\ $$$$ \\ $$$$\:\frac{\mathrm{1}\:+\:\mathrm{2}\boldsymbol{{y}}^{\mathrm{2}} }{\boldsymbol{{y}}}\:\boldsymbol{{dy}}\:=\:\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)\:\boldsymbol{{dx}} \\ $$$$ \\ $$$$\boldsymbol{{ln}}\mid\:\boldsymbol{{y}}\:\mid\:+\:\boldsymbol{{y}}^{\mathrm{2}} \:=\:\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)\:+\:\boldsymbol{{c}} \\ $$$$ \\ $$$$\therefore\:\boldsymbol{{y}}^{\mathrm{2}} \:+\:\boldsymbol{{ln}}\:\mid\:\boldsymbol{{y}}\:\mid\:−\:\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)\:=\:\boldsymbol{{c}}\: \\ $$$$ \\ $$$$\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$
Commented by SANOGO last updated on 22/Sep/21

$${merci}\:{bien}\: \\ $$
