Question Number 103788 by bemath last updated on 17/Jul/20
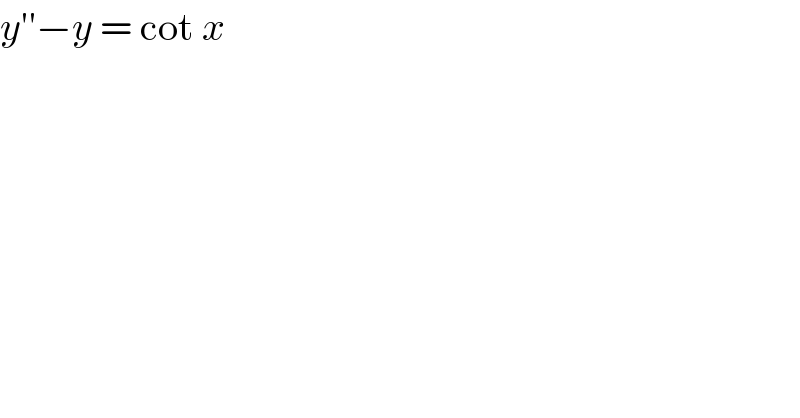
$${y}''−{y}\:=\:\mathrm{cot}\:{x}\: \\ $$
Answered by mathmax by abdo last updated on 18/Jul/20
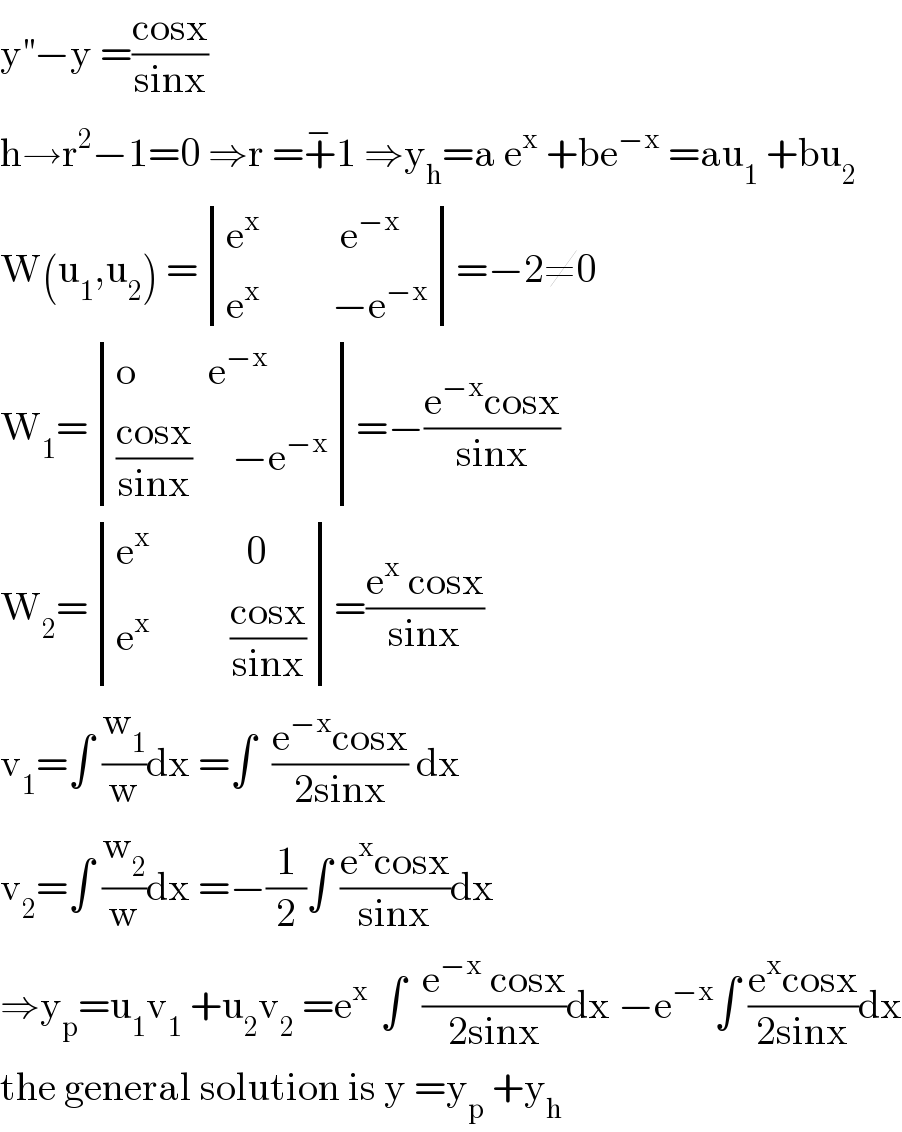
$$\mathrm{y}^{''} −\mathrm{y}\:=\frac{\mathrm{cosx}}{\mathrm{sinx}} \\ $$$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{r}\:=\overset{−} {+}\mathrm{1}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{a}\:\mathrm{e}^{\mathrm{x}} \:+\mathrm{be}^{−\mathrm{x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:−\mathrm{e}^{−\mathrm{x}} }\end{vmatrix}=−\mathrm{2}\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{x}} }\\{\frac{\mathrm{cosx}}{\mathrm{sinx}}\:\:\:\:\:−\mathrm{e}^{−\mathrm{x}} }\end{vmatrix}=−\frac{\mathrm{e}^{−\mathrm{x}} \mathrm{cosx}}{\mathrm{sinx}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\frac{\mathrm{cosx}}{\mathrm{sinx}}}\end{vmatrix}=\frac{\mathrm{e}^{\mathrm{x}} \:\mathrm{cosx}}{\mathrm{sinx}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{e}^{−\mathrm{x}} \mathrm{cosx}}{\mathrm{2sinx}}\:\mathrm{dx} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{e}^{\mathrm{x}} \mathrm{cosx}}{\mathrm{sinx}}\mathrm{dx} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \:=\mathrm{e}^{\mathrm{x}\:} \:\int\:\:\frac{\mathrm{e}^{−\mathrm{x}} \:\mathrm{cosx}}{\mathrm{2sinx}}\mathrm{dx}\:−\mathrm{e}^{−\mathrm{x}} \int\:\frac{\mathrm{e}^{\mathrm{x}} \mathrm{cosx}}{\mathrm{2sinx}}\mathrm{dx} \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{p}} \:+\mathrm{y}_{\mathrm{h}} \\ $$
