Question Number 156744 by joki last updated on 15/Oct/21
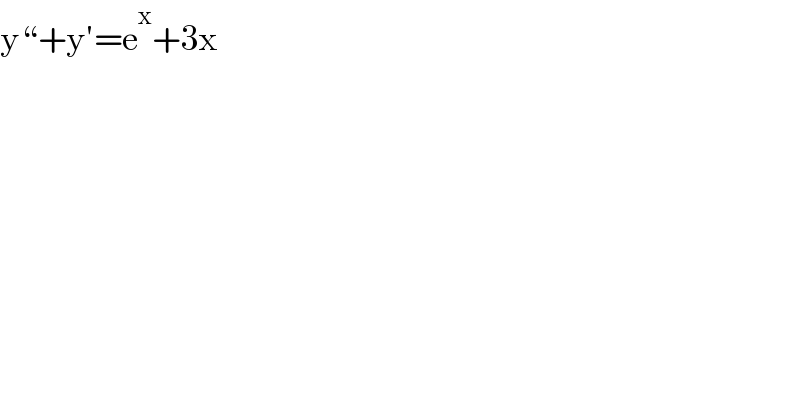
$$\mathrm{y}“+\mathrm{y}'=\mathrm{e}^{\mathrm{x}} +\mathrm{3x} \\ $$$$ \\ $$
Answered by qaz last updated on 15/Oct/21
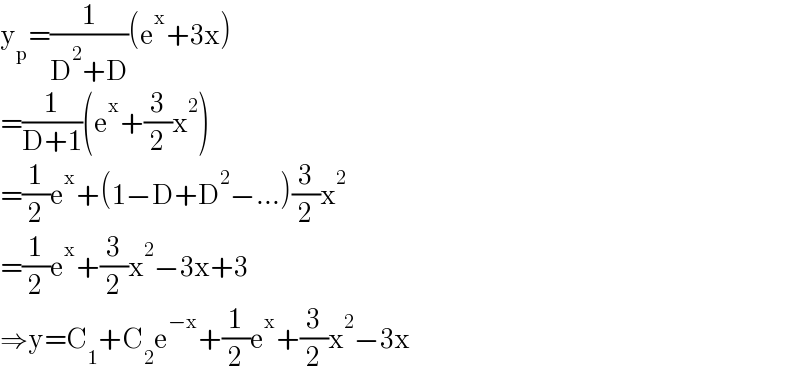
$$\mathrm{y}_{\mathrm{p}} =\frac{\mathrm{1}}{\mathrm{D}^{\mathrm{2}} +\mathrm{D}}\left(\mathrm{e}^{\mathrm{x}} +\mathrm{3x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{D}+\mathrm{1}}\left(\mathrm{e}^{\mathrm{x}} +\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} +\left(\mathrm{1}−\mathrm{D}+\mathrm{D}^{\mathrm{2}} −…\right)\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} +\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{3} \\ $$$$\Rightarrow\mathrm{y}=\mathrm{C}_{\mathrm{1}} +\mathrm{C}_{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} +\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} −\mathrm{3x} \\ $$
Commented by puissant last updated on 15/Oct/21
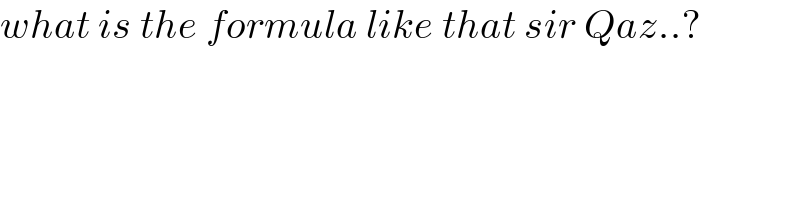
$${what}\:{is}\:{the}\:{formula}\:{like}\:{that}\:{sir}\:{Qaz}..? \\ $$
Answered by mathmax by abdo last updated on 16/Oct/21
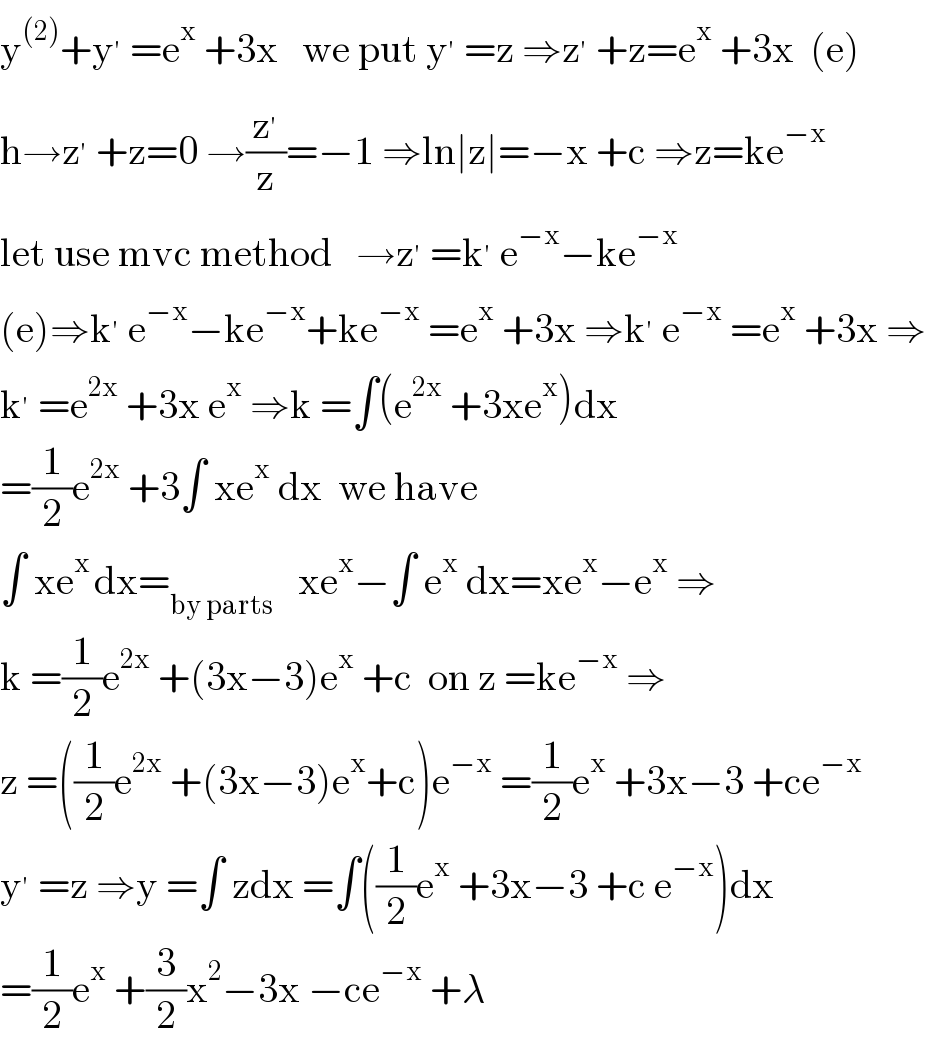
$$\mathrm{y}^{\left(\mathrm{2}\right)} +\mathrm{y}^{'} \:=\mathrm{e}^{\mathrm{x}} \:+\mathrm{3x}\:\:\:\mathrm{we}\:\mathrm{put}\:\mathrm{y}^{'} \:=\mathrm{z}\:\Rightarrow\mathrm{z}^{'} \:+\mathrm{z}=\mathrm{e}^{\mathrm{x}} \:+\mathrm{3x}\:\:\left(\mathrm{e}\right) \\ $$$$\mathrm{h}\rightarrow\mathrm{z}^{'} \:+\mathrm{z}=\mathrm{0}\:\rightarrow\frac{\mathrm{z}^{'} }{\mathrm{z}}=−\mathrm{1}\:\Rightarrow\mathrm{ln}\mid\mathrm{z}\mid=−\mathrm{x}\:+\mathrm{c}\:\Rightarrow\mathrm{z}=\mathrm{ke}^{−\mathrm{x}} \\ $$$$\mathrm{let}\:\mathrm{use}\:\mathrm{mvc}\:\mathrm{method}\:\:\:\rightarrow\mathrm{z}^{'} \:=\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{x}} −\mathrm{ke}^{−\mathrm{x}} \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{x}} −\mathrm{ke}^{−\mathrm{x}} +\mathrm{ke}^{−\mathrm{x}} \:=\mathrm{e}^{\mathrm{x}} \:+\mathrm{3x}\:\Rightarrow\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{x}} \:=\mathrm{e}^{\mathrm{x}} \:+\mathrm{3x}\:\Rightarrow \\ $$$$\mathrm{k}^{'} \:=\mathrm{e}^{\mathrm{2x}} \:+\mathrm{3x}\:\mathrm{e}^{\mathrm{x}} \:\Rightarrow\mathrm{k}\:=\int\left(\mathrm{e}^{\mathrm{2x}} \:+\mathrm{3xe}^{\mathrm{x}} \right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \:+\mathrm{3}\int\:\mathrm{xe}^{\mathrm{x}} \:\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\int\:\mathrm{xe}^{\mathrm{x}\:} \mathrm{dx}=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\mathrm{xe}^{\mathrm{x}} −\int\:\mathrm{e}^{\mathrm{x}} \:\mathrm{dx}=\mathrm{xe}^{\mathrm{x}} −\mathrm{e}^{\mathrm{x}} \:\Rightarrow \\ $$$$\mathrm{k}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \:+\left(\mathrm{3x}−\mathrm{3}\right)\mathrm{e}^{\mathrm{x}} \:+\mathrm{c}\:\:\mathrm{on}\:\mathrm{z}\:=\mathrm{ke}^{−\mathrm{x}} \:\Rightarrow \\ $$$$\mathrm{z}\:=\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \:+\left(\mathrm{3x}−\mathrm{3}\right)\mathrm{e}^{\mathrm{x}} +\mathrm{c}\right)\mathrm{e}^{−\mathrm{x}} \:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} \:+\mathrm{3x}−\mathrm{3}\:+\mathrm{ce}^{−\mathrm{x}} \\ $$$$\mathrm{y}^{'} \:=\mathrm{z}\:\Rightarrow\mathrm{y}\:=\int\:\mathrm{zdx}\:=\int\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} \:+\mathrm{3x}−\mathrm{3}\:+\mathrm{c}\:\mathrm{e}^{−\mathrm{x}} \right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} \:+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} −\mathrm{3x}\:−\mathrm{ce}^{−\mathrm{x}} \:+\lambda \\ $$
