y-y-e-x-e-x-e-x-

Question Number 103014 by bobhans last updated on 12/Jul/20

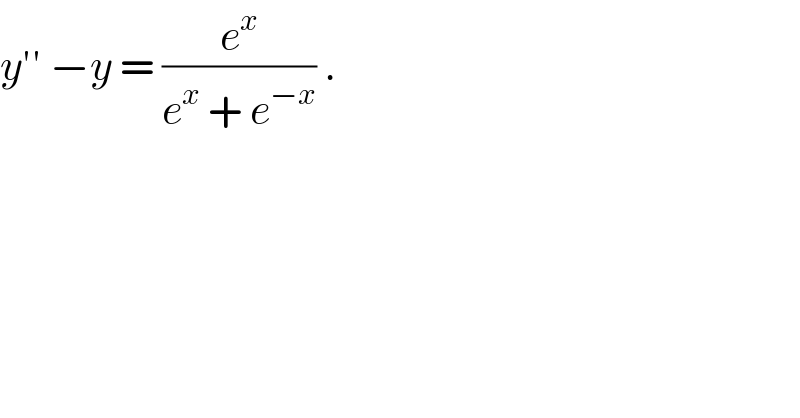
y^{″} - y = \frac{e^{x}}{e^{x} + e^{- x}} .

Answered by bobhans last updated on 12/Jul/20

t h e c h a r a c t e r i s t i c e q u a t i o n o f t h e

h o m o g e n o u s e q u a t i o n i s γ^{2} - 1 = 0; γ = \pm 1

y_{h} = C_{1} e^{x} + C_{2} e^{- x}

s a y y_{1} (x) = e^{x} \to y_{1}^{'} = e^{x}

y_{2} (x) = e^{- x} \to y_{2}^{'} = - e^{- x}

W r o n s k i a n W (y_{1}, y_{2}) = | \begin{matrix} y_{1} y_{2} \\ y_{1}^{'} y_{2}^{'} \end{matrix} | =

| \begin{matrix} e^{x} e^{- x} \\ e^{x} - e^{- x} \end{matrix} | = - 2 \neq 0

I_{1} = \int \frac{e^{x} (\frac{e^{x}}{e^{x} + e^{- x}})}{W (y_{1}, y_{2})} d x = - \frac{1}{2} \int \frac{e^{2 x}}{e^{x} + e^{- x}} d x

= - \frac{1}{2} e^{x} + \frac{1}{2} \tan^{- 1} (e^{x})

I_{2} = \int \frac{e^{- x} (\frac{e^{x}}{e^{x} + e^{- x}})}{- 2} d x = - \frac{1}{2} \int \frac{d x}{e^{x} + e^{- x}}

= - \frac{1}{2} \tan^{- 1} (e^{x})

y_{p} = - e^{x} I_{2} + e^{- x} I_{1} = \frac{1}{2} e^{x} \tan^{- 1} (e^{x}) -

\frac{1}{2} + \frac{1}{2} e^{- x} \tan^{- 1} (e^{x})

c o m p l e t e s o l u t i o n

y = C_{1} e^{x} + C_{2} e^{- x} + \frac{1}{2} (e^{x} + e^{- x}) \tan^{- 1} (e^{x}) - \frac{1}{2}

Commented by bramlex last updated on 12/Jul/20

coll joss

Answered by mathmax by abdo last updated on 12/Jul/20

y^{^{″}} - y = \frac{e^{x}}{e^{x} + e^{- x}}

(he) \to y^{^{″}} - y = 0 \to r^{2} - 1 = 0 \to r = \bar{+} 1 \Rightarrow y_{h} = a e^{x} + {be}^{- x} = {au}_{1} + {bu}_{2}

W (u_{1}, u_{2}) = | \begin{matrix} e^{x} e^{- x} \\ e^{x} - e^{- x} \end{matrix} | = - 2 \neq 0

W_{1} = | \begin{matrix} o e^{- x} \\ \frac{e^{x}}{e^{x} + e^{- x}} - e^{- x} \end{matrix} | = - \frac{1}{e^{x} + e^{- x}}

W_{2} = | \begin{matrix} e^{x} 0 \\ e^{x} \frac{e^{x}}{e^{x} + e^{- x}} \end{matrix} | = \frac{e^{2 x}}{e^{x} + e^{- x}}

v_{1} = \int \frac{W_{1}}{W} dx = \int \frac{dx}{2 (e^{x} + e^{- x})} =_{e^{x} = t} \frac{1}{2} \int \frac{dt}{t (t + t^{- 1})} = \frac{1}{2} \int \frac{dt}{t^{2} + 1}

= \frac{1}{2} \arctan (t) = \frac{1}{2} \arctan (e^{x})

v_{2} = \int \frac{W_{2}}{W} dx = - \int \frac{e^{2 x}}{2 (e^{x} + e^{- x})} dx =_{e^{x} = t} - \frac{1}{2} \int \frac{t^{2}}{t (t + t^{- 1})} dt

= - \frac{1}{2} \int \frac{t}{t + t^{- 1}} dt = - \frac{1}{2} \int \frac{t^{2}}{t^{2} + 1} dx = - \frac{1}{2} \int \frac{t^{2} + 1 - 1}{t^{2} + 1} dt

= - \frac{1}{2} t + \frac{1}{2} \arctan (t) = - \frac{e^{x}}{2} + \frac{1}{2} \arctan (e^{x}) \Rightarrow

y_{p} = u_{1} v_{1} + u_{2} v_{2} = e^{x} (\frac{1}{2} \arctan (e^{x})) + e^{- x} (- \frac{e^{x}}{2} + \frac{1}{2} \arctan (e^{x}))

= \frac{e^{x}}{2} \arctan (e^{x}) - \frac{1}{2} + \frac{e^{- x}}{2} \arctan (e^{x})

= ch (x) \arctan (e^{x}) - \frac{1}{2} the general solution is

y = y_{h} + y_{p} = {ae}^{x} + {be}^{- x} + ch (x) \arctan (e^{x}) - \frac{1}{2}