Menu Close

y-y-x-2-1-y-2-

Tinku Tara 0 Comments
Pin




Question Number 103776 by bemath last updated on 17/Jul/20
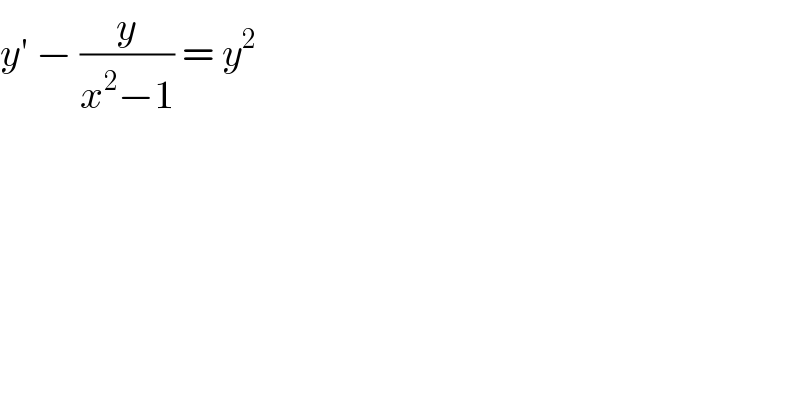
y′ − (y/(x^2 −1)) = y^2
$${y}'\:−\:\frac{{y}}{{x}^{\mathrm{2}} −\mathrm{1}}\:=\:{y}^{\mathrm{2}} \\ $$
Answered by bemath last updated on 17/Jul/20
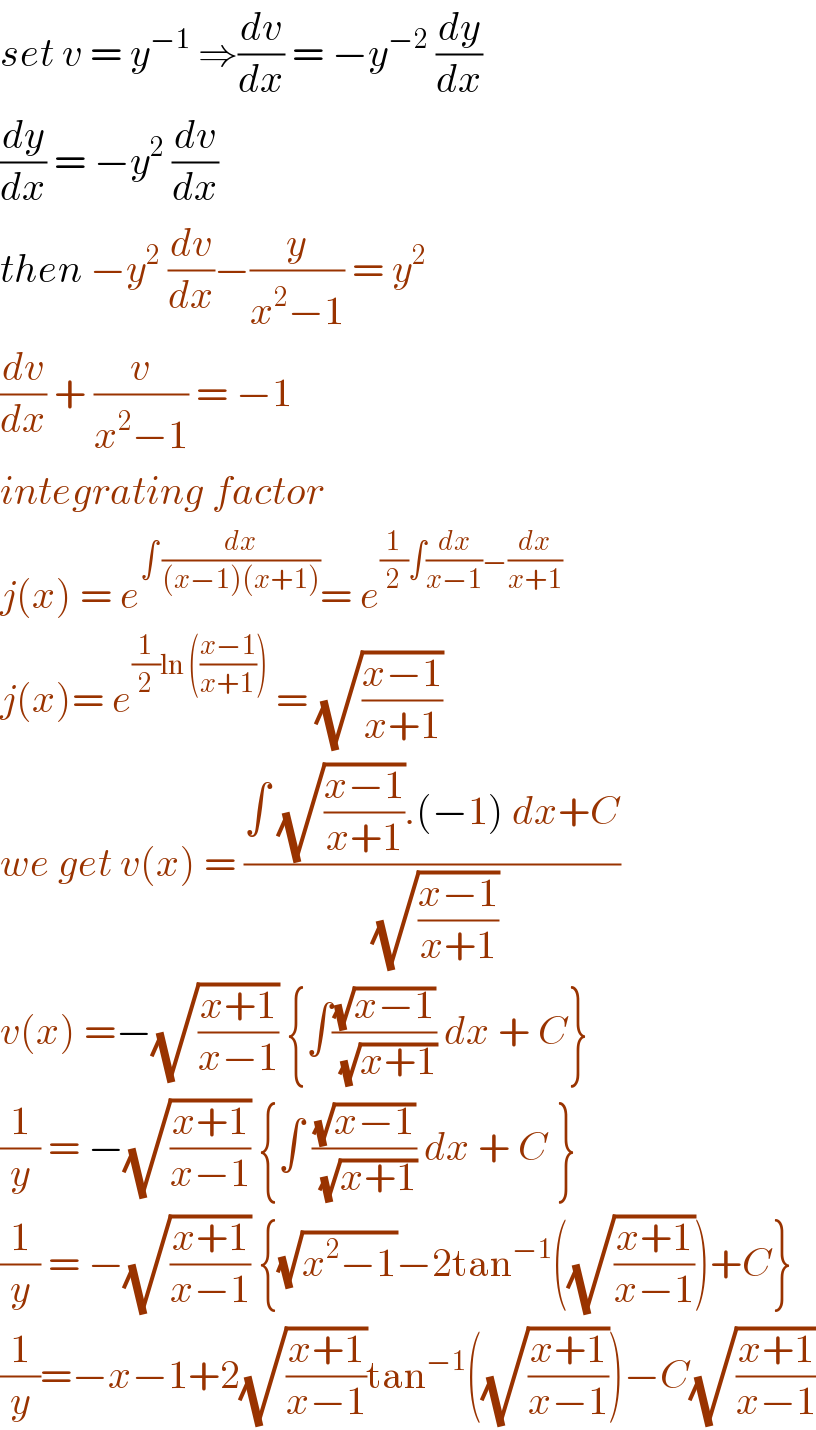
set v = y^(−1) ⇒(dv/dx) = −y^(−2) (dy/dx) (dy/dx) = −y^2 (dv/dx) then −y^2 (dv/dx)−(y/(x^2 −1)) = y^2 (dv/dx) + (v/(x^2 −1)) = −1 integrating factor j(x) = e^(∫ (dx/((x−1)(x+1)))) = e^((1/2)∫(dx/(x−1))−(dx/(x+1))) j(x)= e^((1/2)ln (((x−1)/(x+1)))) = (√((x−1)/(x+1))) we get v(x) = ((∫ (√((x−1)/(x+1))).(−1) dx+C)/( (√((x−1)/(x+1))))) v(x) =−(√((x+1)/(x−1))) {∫((√(x−1))/( (√(x+1)))) dx + C} (1/y) = −(√((x+1)/(x−1))) {∫ ((√(x−1))/( (√(x+1)))) dx + C } (1/y) = −(√((x+1)/(x−1))) {(√(x^2 −1))−2tan^(−1) ((√((x+1)/(x−1))))+C} (1/y)=−x−1+2(√((x+1)/(x−1)))tan^(−1) ((√((x+1)/(x−1))))−C(√((x+1)/(x−1)))
$${set}\:{v}\:=\:{y}^{−\mathrm{1}} \:\Rightarrow\frac{{dv}}{{dx}}\:=\:−{y}^{−\mathrm{2}} \:\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}\:=\:−{y}^{\mathrm{2}} \:\frac{{dv}}{{dx}} \\ $$$${then}\:−{y}^{\mathrm{2}} \:\frac{{dv}}{{dx}}−\frac{{y}}{{x}^{\mathrm{2}} −\mathrm{1}}\:=\:{y}^{\mathrm{2}} \\ $$$$\frac{{dv}}{{dx}}\:+\:\frac{{v}}{{x}^{\mathrm{2}} −\mathrm{1}}\:=\:−\mathrm{1} \\ $$$${integrating}\:{factor}\: \\ $$$${j}\left({x}\right)\:=\:{e}^{\int\:\frac{{dx}}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}} =\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}−\mathrm{1}}−\frac{{dx}}{{x}+\mathrm{1}}} \\ $$$${j}\left({x}\right)=\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)} \:=\:\sqrt{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}} \\ $$$${we}\:{get}\:{v}\left({x}\right)\:=\:\frac{\int\:\sqrt{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}}.\left(−\mathrm{1}\right)\:{dx}+{C}}{\:\sqrt{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}}} \\ $$$${v}\left({x}\right)\:=−\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}\:\left\{\int\frac{\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}+\mathrm{1}}}\:{dx}\:+\:{C}\right\}\: \\ $$$$\frac{\mathrm{1}}{{y}}\:=\:−\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}\:\left\{\int\:\frac{\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}+\mathrm{1}}}\:{dx}\:+\:{C}\:\right\} \\ $$$$\frac{\mathrm{1}}{{y}}\:=\:−\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}\:\left\{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−\mathrm{2tan}^{−\mathrm{1}} \left(\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}\right)+{C}\right\} \\ $$$$\frac{\mathrm{1}}{{y}}=−{x}−\mathrm{1}+\mathrm{2}\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}\right)−{C}\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}} \\ $$
Commented by Ar Brandon last updated on 17/Jul/20
What's the secret to knowing the right change of variable to use ? ��
Commented by bobhans last updated on 17/Jul/20
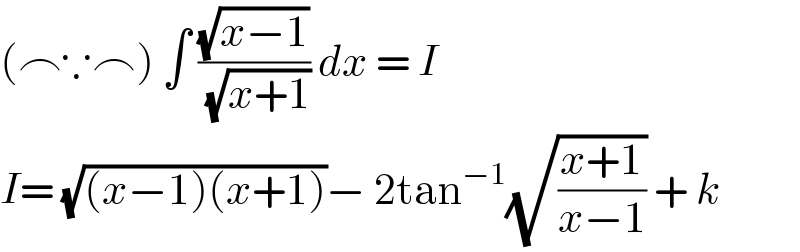
(⌢∵⌢) ∫ ((√(x−1))/( (√(x+1)))) dx = I I= (√((x−1)(x+1)))− 2tan^(−1) (√((x+1)/(x−1))) + k
$$\left(\frown\because\frown\right)\:\int\:\frac{\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}+\mathrm{1}}}\:{dx}\:=\:{I} \\ $$$${I}=\:\sqrt{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}−\:\mathrm{2tan}^{−\mathrm{1}} \sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}\:+\:{k}\: \\ $$
Commented by bemath last updated on 17/Jul/20
Bernoulli eq sir
$${Bernoulli}\:{eq}\:{sir} \\ $$
Commented by Coronavirus last updated on 17/Jul/20
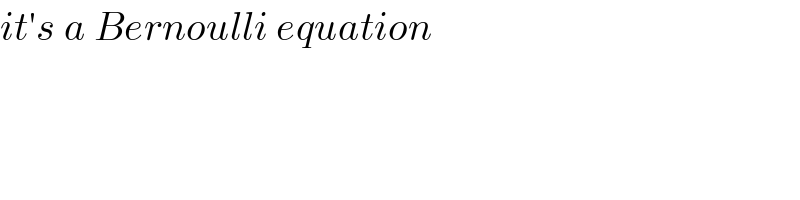
it′s a Bernoulli equation
$${it}'{s}\:{a}\:{Bernoulli}\:{equation} \\ $$
Answered by mathmax by abdo last updated on 17/Jul/20
e⇒y^′ −(1/(x^2 −1))y =y^2 ⇒(y^′ /y^2 )−(1/(x^2 −1))×(1/y) =1 let z =(1/y) ⇒y =(1/z) ⇒y^′ =−(z^′ /z^2 ) e⇒−(z^′ /z^2 )×z^2 −(1/(x^2 −1))×z =1 ⇒−z^′ −(1/(x^2 −1))z =1 ⇒z^′ +(z/(x^2 −1)) =−1 e^, he→z^′ =−(z/(x^2 −1)) ⇒(z^′ /z) =−(1/(x^2 −1)) ⇒ln∣z∣ =−∫ (dx/(x^2 −1)) =−(1/2)∫((1/(x−1))−(1/(x+1)))dx =−(1/2)ln∣((x−1)/(x+1))∣ +c =(1/2)ln∣((x+1)/(x−1))∣ +c ⇒z =k (√(∣((x+1)/(x−1))∣)) solution on w ={x/((x+1)/(x−1))>0} mvc method →z^′ =k^′ (√((x+1)/(x−1))) +k ×(((((x+1)/(x−1)))^′ )/(2(√((x+1)/(x−1))))) =k^′ (√((x+1)/(x−1)))+(k/2)×((−2)/((x−1)^2 (√((x+1)/(x−1))))) e^′ ⇒ k^′ (√((x+1)/(x−1)))−(k/((x−1)^2 (√((x+1)/(x−1))))) +(1/(x^2 −1))×k(√(((x+1)/(x−1)) ))=−1 ⇒ k^′ =−(√((x−1)/(x+1))) ⇒k =−∫ (√((x−1)/(x+1)))dx changement (√((x−1)/(x+1)))=t give ((x−1)/(x+1))=t^2 ⇒x−1 =t^2 x+t^2 ⇒(1−t^2 )x =t^2 +1 ⇒x =((t^2 +1)/(1−t^2 )) dx =((2t(1−t^2 )−(t^2 +1)(−2t))/((1−t^2 )^2 ))dt =((2t−2t^3 +2t^3 +2t)/((t^2 −1)^2 ))dt =((4tdt)/((t^2 −1)^2 )) ⇒ ∫ (√((x−1)/(x+1)))dx =4 ∫ ((tdt)/((t^2 −1)^2 )) =4 ∫ ((tdt)/((t−1)^2 (t+1)^2 )) =4 ∫ ((tdt)/((((t−1)/(t+1)))^2 (t+1)^4 )) we do the changement ((t−1)/(t+1))=z ⇒t−1 =zt+z ⇒ (1−z)t=1+z ⇒t =((1+z)/(1−z)) ⇒(dt/dz) =((1−z+(1+z))/((1−z)^2 )) =(2/((1−z)^2 )) t+1 =((1+z)/(1−z)) +1 =((1+z+1−z)/(1−z)) =(2/(1−z)) ⇒I= ∫ ((1+z)/(1−z))×(2/((1−z)^2 z^2 ((2/(1−z)))^4 ))dz =(1/8)∫ (((1+z)(1−z)^4 )/((1−z)^3 ))dz =(1/8)∫ (1−z^2 )dz =(1/8)(z−(z^3 /3)) +c =(1/8)(((t−1)/(t+1)))−(1/(24))(((t−1)/(t+1)))^3 +c with t =(√((x−1)/(x+1))) y(x)=(1/(z(x)))
$$\mathrm{e}\Rightarrow\mathrm{y}^{'} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\mathrm{y}\:=\mathrm{y}^{\mathrm{2}} \:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}×\frac{\mathrm{1}}{\mathrm{y}}\:=\mathrm{1}\:\:\mathrm{let}\:\mathrm{z}\:=\frac{\mathrm{1}}{\mathrm{y}}\:\Rightarrow\mathrm{y}\:=\frac{\mathrm{1}}{\mathrm{z}} \\ $$$$\Rightarrow\mathrm{y}^{'} \:=−\frac{\mathrm{z}^{'} }{\mathrm{z}^{\mathrm{2}} } \\ $$$$\mathrm{e}\Rightarrow−\frac{\mathrm{z}^{'} }{\mathrm{z}^{\mathrm{2}} }×\mathrm{z}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}×\mathrm{z}\:=\mathrm{1}\:\Rightarrow−\mathrm{z}^{'} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\mathrm{z}\:=\mathrm{1}\:\Rightarrow\mathrm{z}^{'} +\frac{\mathrm{z}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:=−\mathrm{1}\:\:\mathrm{e}^{,} \\ $$$$\mathrm{he}\rightarrow\mathrm{z}^{'} \:=−\frac{\mathrm{z}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow\frac{\mathrm{z}^{'} }{\mathrm{z}}\:=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow\mathrm{ln}\mid\mathrm{z}\mid\:=−\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\mid\:+\mathrm{c}\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\mid\:+\mathrm{c}\:\Rightarrow\mathrm{z}\:=\mathrm{k}\:\sqrt{\mid\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\mid} \\ $$$$\mathrm{solution}\:\:\mathrm{on}\:\mathrm{w}\:=\left\{\mathrm{x}/\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}>\mathrm{0}\right\}\:\mathrm{mvc}\:\mathrm{method}\:\rightarrow\mathrm{z}^{'} \:=\mathrm{k}^{'} \sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}} \\ $$$$+\mathrm{k}\:×\frac{\left(\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right)^{'} }{\mathrm{2}\sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}}}\:=\mathrm{k}^{'} \sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}}+\frac{\mathrm{k}}{\mathrm{2}}×\frac{−\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}}} \\ $$$$\mathrm{e}^{'} \:\Rightarrow\:\mathrm{k}^{'} \sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}}−\frac{\mathrm{k}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}}}\:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}×\mathrm{k}\sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}\:}=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{k}^{'} \:=−\sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}}\:\Rightarrow\mathrm{k}\:=−\int\:\sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}}\mathrm{dx}\:\:\mathrm{changement}\:\sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}}=\mathrm{t}\:\mathrm{give} \\ $$$$\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}−\mathrm{1}\:=\mathrm{t}^{\mathrm{2}} \mathrm{x}+\mathrm{t}^{\mathrm{2}} \:\Rightarrow\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\mathrm{x}\:=\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow\mathrm{x}\:=\frac{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} } \\ $$$$\mathrm{dx}\:=\frac{\mathrm{2t}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)−\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(−\mathrm{2t}\right)}{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\:=\frac{\mathrm{2t}−\mathrm{2t}^{\mathrm{3}} +\mathrm{2t}^{\mathrm{3}} \:+\mathrm{2t}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}\:=\frac{\mathrm{4tdt}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:\sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}}\mathrm{dx}\:=\mathrm{4}\:\int\:\frac{\mathrm{tdt}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\:=\mathrm{4}\:\int\:\:\frac{\mathrm{tdt}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{4}\:\int\:\:\frac{\mathrm{tdt}}{\left(\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)^{\mathrm{2}} \left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{4}} }\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}=\mathrm{z}\:\Rightarrow\mathrm{t}−\mathrm{1}\:=\mathrm{zt}+\mathrm{z}\:\Rightarrow \\ $$$$\left(\mathrm{1}−\mathrm{z}\right)\mathrm{t}=\mathrm{1}+\mathrm{z}\:\Rightarrow\mathrm{t}\:=\frac{\mathrm{1}+\mathrm{z}}{\mathrm{1}−\mathrm{z}}\:\Rightarrow\frac{\mathrm{dt}}{\mathrm{dz}}\:=\frac{\mathrm{1}−\mathrm{z}+\left(\mathrm{1}+\mathrm{z}\right)}{\left(\mathrm{1}−\mathrm{z}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{z}\right)^{\mathrm{2}} } \\ $$$$\mathrm{t}+\mathrm{1}\:=\frac{\mathrm{1}+\mathrm{z}}{\mathrm{1}−\mathrm{z}}\:+\mathrm{1}\:=\frac{\mathrm{1}+\mathrm{z}+\mathrm{1}−\mathrm{z}}{\mathrm{1}−\mathrm{z}}\:=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{z}}\:\Rightarrow\mathrm{I}=\:\int\:\frac{\mathrm{1}+\mathrm{z}}{\mathrm{1}−\mathrm{z}}×\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{z}\right)^{\mathrm{2}} \mathrm{z}^{\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{1}−\mathrm{z}}\right)^{\mathrm{4}} }\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\:\:\:\:\frac{\left(\mathrm{1}+\mathrm{z}\right)\left(\mathrm{1}−\mathrm{z}\right)^{\mathrm{4}} }{\left(\mathrm{1}−\mathrm{z}\right)^{\mathrm{3}} }\mathrm{dz}\:=\frac{\mathrm{1}}{\mathrm{8}}\int\:\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{z}−\frac{\mathrm{z}^{\mathrm{3}} }{\mathrm{3}}\right)\:+\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{24}}\left(\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)^{\mathrm{3}} \:+\mathrm{c}\:\:\mathrm{with}\:\mathrm{t}\:=\sqrt{\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{z}\left(\mathrm{x}\right)} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *