y-y-x-y-2-1-3-

Question Number 96065 by john santu last updated on 29/May/20

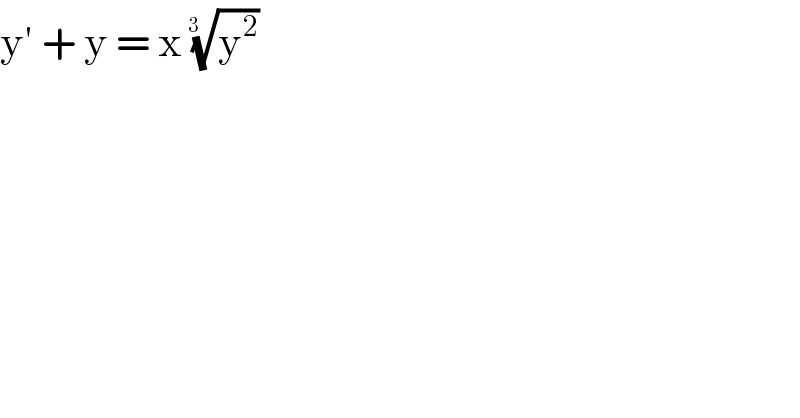
$$\mathrm{y}'\:+\:\mathrm{y}\:=\:\mathrm{x}\:\sqrt[{\mathrm{3}\:\:}]{\mathrm{y}^{\mathrm{2}} } \\ $$

Answered by bobhans last updated on 29/May/20

Bernoulli eq v = y^(1−(2/3)) = y^(1/3) ⇒ (dv/dx) = (1/3)y^(−(2/3)) .(dy/dx) (dy/dx) = 3y^(2/3) (dv/dx) ⇒ 3y^(2/3) v′+y= xy^(2/3) v′ + (1/3)v = (1/3)x. integrating factor u(x) = e^(∫ (1/3) dx ) u(x) = e^((1/3)x) ⇒ e^((1/3)x) v =∫ (1/3)xe^((1/3)x) dx 3e^((1/3)x) y^(1/3) = xe^((1/3)x) −3e^((1/3)x) + C y^(1/3) = (1/3)x−1+Ce^(−(1/3)x) •.

$$\mathrm{Bernoulli}\:\mathrm{eq}\: \\ $$$$\mathrm{v}\:=\:\mathrm{y}^{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}} \:=\:\mathrm{y}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\Rightarrow\:\frac{\mathrm{dv}}{\mathrm{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{y}^{−\frac{\mathrm{2}}{\mathrm{3}}} .\frac{\mathrm{dy}}{\mathrm{dx}} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{3y}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\Rightarrow\:\mathrm{3y}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\mathrm{v}'+\mathrm{y}=\:\mathrm{xy}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\mathrm{v}'\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{v}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}.\: \\ $$$$\mathrm{integrating}\:\mathrm{factor}\:\mathrm{u}\left(\mathrm{x}\right)\:=\:\mathrm{e}^{\int\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{dx}\:} \\ $$$$\mathrm{u}\left(\mathrm{x}\right)\:=\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}} \:\Rightarrow\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}} \mathrm{v}\:=\int\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{xe}^{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}} \:\mathrm{dx}\: \\ $$$$\mathrm{3e}^{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}} \mathrm{y}^{\frac{\mathrm{1}}{\mathrm{3}}} \:=\:\mathrm{xe}^{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}} −\mathrm{3e}^{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}} +\:\mathrm{C} \\ $$$$\mathrm{y}^{\frac{\mathrm{1}}{\mathrm{3}}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}−\mathrm{1}+\mathrm{Ce}^{−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}} \:\bullet.\: \\ $$

Commented by john santu last updated on 29/May/20

��

Answered by abdomathmax last updated on 29/May/20

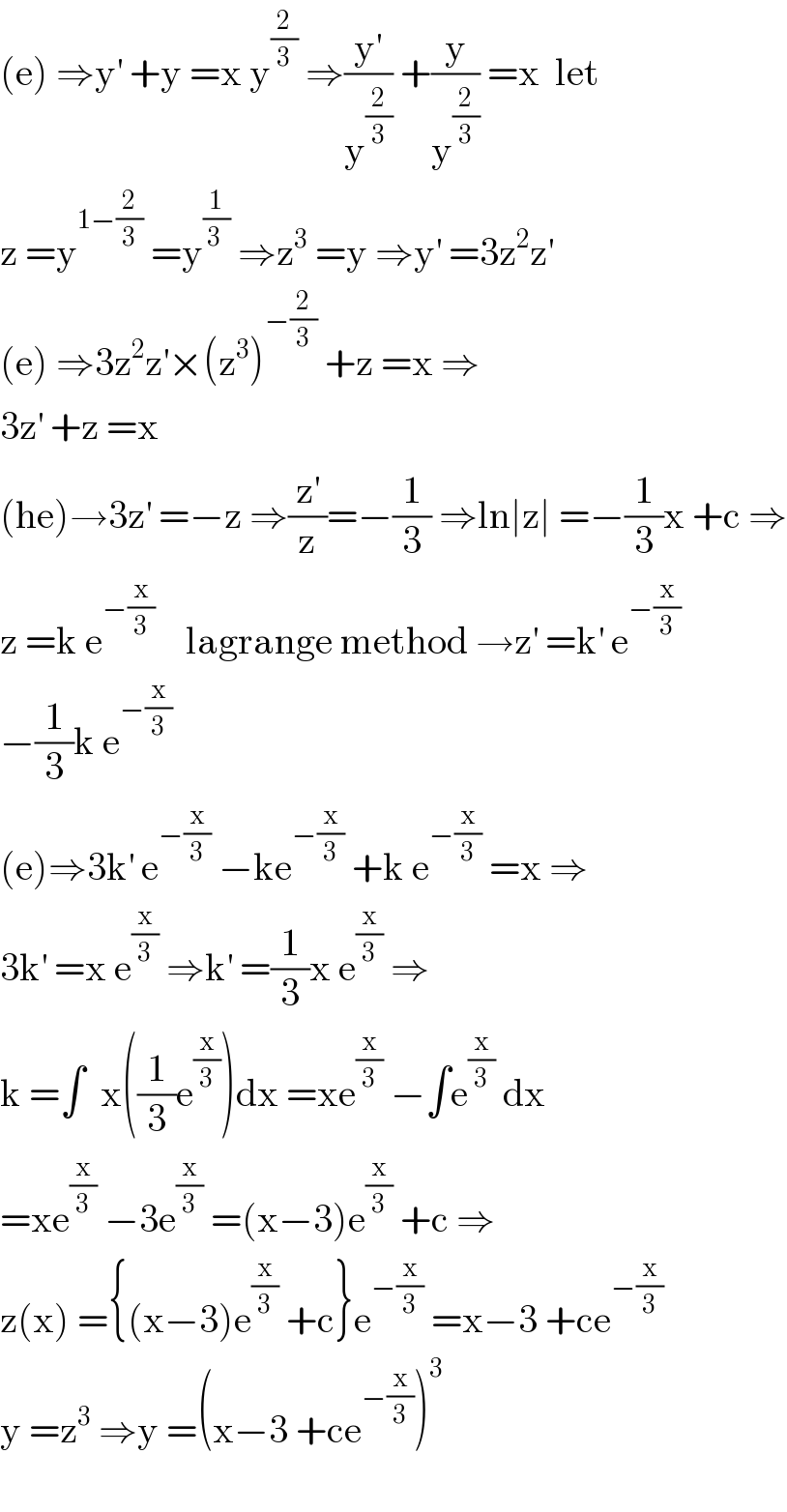
(e) ⇒y^′ +y =x y^(2/3) ⇒(y^′ /y^(2/3) ) +(y/y^(2/3) ) =x let z =y^(1−(2/3)) =y^(1/(3 )) ⇒z^3 =y ⇒y^′ =3z^2 z^′ (e) ⇒3z^2 z^′ ×(z^3 )^(−(2/3)) +z =x ⇒ 3z^′ +z =x (he)→3z^′ =−z ⇒(z^′ /z)=−(1/3) ⇒ln∣z∣ =−(1/3)x +c ⇒ z =k e^(−(x/3)) lagrange method →z^′ =k^′ e^(−(x/3)) −(1/3)k e^(−(x/3)) (e)⇒3k^′ e^(−(x/3)) −ke^(−(x/3)) +k e^(−(x/3)) =x ⇒ 3k^′ =x e^(x/3) ⇒k^′ =(1/3)x e^(x/3) ⇒ k =∫ x((1/3)e^(x/3) )dx =xe^(x/3) −∫e^(x/3) dx =xe^(x/3) −3e^(x/3) =(x−3)e^(x/3) +c ⇒ z(x) ={(x−3)e^(x/3) +c}e^(−(x/3)) =x−3 +ce^(−(x/3)) y =z^3 ⇒y =(x−3 +ce^(−(x/3)) )^3

$$\left(\mathrm{e}\right)\:\Rightarrow\mathrm{y}^{'} \:+\mathrm{y}\:=\mathrm{x}\:\mathrm{y}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:+\frac{\mathrm{y}}{\mathrm{y}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:=\mathrm{x}\:\:\mathrm{let} \\ $$$$\mathrm{z}\:=\mathrm{y}^{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}} \:=\mathrm{y}^{\frac{\mathrm{1}}{\mathrm{3}\:}} \:\Rightarrow\mathrm{z}^{\mathrm{3}} \:=\mathrm{y}\:\Rightarrow\mathrm{y}^{'} \:=\mathrm{3z}^{\mathrm{2}} \mathrm{z}^{'} \\ $$$$\left(\mathrm{e}\right)\:\Rightarrow\mathrm{3z}^{\mathrm{2}} \mathrm{z}^{'} ×\left(\mathrm{z}^{\mathrm{3}} \right)^{−\frac{\mathrm{2}}{\mathrm{3}}} \:+\mathrm{z}\:=\mathrm{x}\:\Rightarrow \\ $$$$\mathrm{3z}^{'} \:+\mathrm{z}\:=\mathrm{x} \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{3z}^{'} \:=−\mathrm{z}\:\Rightarrow\frac{\mathrm{z}^{'} }{\mathrm{z}}=−\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\mathrm{ln}\mid\mathrm{z}\mid\:=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{z}\:=\mathrm{k}\:\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{3}}} \:\:\:\:\mathrm{lagrange}\:\mathrm{method}\:\rightarrow\mathrm{z}^{'} \:=\mathrm{k}^{'} \:\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{3}}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{k}\:\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{3}}} \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{3k}^{'} \:\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{3}}} \:−\mathrm{ke}^{−\frac{\mathrm{x}}{\mathrm{3}}} \:+\mathrm{k}\:\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{3}}} \:=\mathrm{x}\:\Rightarrow \\ $$$$\mathrm{3k}^{'} \:=\mathrm{x}\:\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{3}}} \:\Rightarrow\mathrm{k}^{'} \:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}\:\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{3}}} \:\Rightarrow \\ $$$$\mathrm{k}\:=\int\:\:\mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{3}}} \right)\mathrm{dx}\:=\mathrm{xe}^{\frac{\mathrm{x}}{\mathrm{3}}} \:−\int\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{3}}} \:\mathrm{dx} \\ $$$$=\mathrm{xe}^{\frac{\mathrm{x}}{\mathrm{3}}} \:−\mathrm{3e}^{\frac{\mathrm{x}}{\mathrm{3}}} \:=\left(\mathrm{x}−\mathrm{3}\right)\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{3}}} \:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{z}\left(\mathrm{x}\right)\:=\left\{\left(\mathrm{x}−\mathrm{3}\right)\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{3}}} \:+\mathrm{c}\right\}\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{3}}} \:=\mathrm{x}−\mathrm{3}\:+\mathrm{ce}^{−\frac{\mathrm{x}}{\mathrm{3}}} \\ $$$$\mathrm{y}\:=\mathrm{z}^{\mathrm{3}} \:\Rightarrow\mathrm{y}\:=\left(\mathrm{x}−\mathrm{3}\:+\mathrm{ce}^{−\frac{\mathrm{x}}{\mathrm{3}}} \right)^{\mathrm{3}} \\ $$$$ \\ $$

Answered by Sourav mridha last updated on 29/May/20

⇒(y^(1/3) −x)dx+(1/y^(2/3) )dy=0 (∂/∂y)(y^(1/3) −x)=(1/3)y^(−(2/3)) ≠(∂/∂x)(y^(−(2/3)) )=0 so this is not exact differential now:[(1/y^(−(2/3)) )((1/3)y^(−(2/3)) −0)=(1/3)] so I.F=e^(∫(dx/3)) =e^(x/(3 )) multi:withthis we get:e^(x/3) [y^(1/3) −x]dx+e^(x/3) .y^(−(2/3)) dy=0 now:∫_((keeping y as constant)) e^(x/3) [y^(1/3) −x]dx =3e^(x/3) .y^(1/3) −3xe^(x/3) +9e^(x/3) and:∫_((which dosn′t contain x)) (0)dy=0 so the solution is: e^(x/3) [y^(1/3) −x+3]=c

$$\Rightarrow\left(\mathrm{y}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{x}\right)\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{y}^{\frac{\mathrm{2}}{\mathrm{3}}} }\mathrm{dy}=\mathrm{0} \\ $$$$\frac{\partial}{\partial\boldsymbol{{y}}}\left(\boldsymbol{{y}}^{\frac{\mathrm{1}}{\mathrm{3}}} −\boldsymbol{{x}}\right)=\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{{y}}^{−\frac{\mathrm{2}}{\mathrm{3}}} \neq\frac{\partial}{\partial\boldsymbol{{x}}}\left(\boldsymbol{{y}}^{−\frac{\mathrm{2}}{\mathrm{3}}} \right)=\mathrm{0} \\ $$$$\mathrm{so}\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{exact}\:\mathrm{differential} \\ $$$$\mathrm{now}:\left[\frac{\mathrm{1}}{\boldsymbol{{y}}^{−\frac{\mathrm{2}}{\mathrm{3}}} }\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{y}^{−\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{3}}\right] \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}.\mathrm{F}=\boldsymbol{{e}}^{\int\frac{\mathrm{d}\boldsymbol{{x}}}{\mathrm{3}}} =\boldsymbol{{e}}^{\frac{\boldsymbol{{x}}}{\mathrm{3}\:}} \boldsymbol{{multi}}:\mathrm{withthis}\:\boldsymbol{{we}} \\ $$$$\boldsymbol{{get}}:\boldsymbol{{e}}^{\frac{\boldsymbol{{x}}}{\mathrm{3}}} \left[\boldsymbol{{y}}^{\frac{\mathrm{1}}{\mathrm{3}}} −\boldsymbol{{x}}\right]\boldsymbol{{dx}}+\boldsymbol{{e}}^{\frac{\boldsymbol{{x}}}{\mathrm{3}}} .\boldsymbol{{y}}^{−\frac{\mathrm{2}}{\mathrm{3}}} \boldsymbol{{dy}}=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{now}}:\int_{\left(\boldsymbol{{keeping}}\:\boldsymbol{{y}}\:\boldsymbol{\mathrm{as}}\:\boldsymbol{\mathrm{constant}}\right)} \boldsymbol{{e}}^{\frac{\boldsymbol{{x}}}{\mathrm{3}}} \left[\boldsymbol{{y}}^{\frac{\mathrm{1}}{\mathrm{3}}} −\boldsymbol{{x}}\right]\boldsymbol{{dx}} \\ $$$$\:\:\:\:=\mathrm{3}\boldsymbol{\mathrm{e}}^{\frac{\boldsymbol{{x}}}{\mathrm{3}}} .\boldsymbol{{y}}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{3}\boldsymbol{{xe}}^{\frac{\boldsymbol{{x}}}{\mathrm{3}}} +\mathrm{9}\boldsymbol{{e}}^{\frac{\boldsymbol{{x}}}{\mathrm{3}}} \\ $$$$\boldsymbol{\mathrm{and}}:\int_{\left(\boldsymbol{\mathrm{which}}\:\boldsymbol{\mathrm{dos}}\mathrm{n}'\mathrm{t}\:\boldsymbol{\mathrm{contain}}\:\boldsymbol{\mathrm{x}}\right)} \left(\mathrm{0}\right)\boldsymbol{\mathrm{dy}}=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{is}}: \\ $$$$\:\:\:\:\mathrm{e}^{\frac{\boldsymbol{{x}}}{\mathrm{3}}} \left[\boldsymbol{{y}}^{\frac{\mathrm{1}}{\mathrm{3}}} −\boldsymbol{{x}}+\mathrm{3}\right]=\boldsymbol{{c}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply