Menu Close

y-y-x-y-x-y-0-0-

Tinku Tara 0 Comments
Pin




Question Number 104857 by ~blr237~ last updated on 24/Jul/20
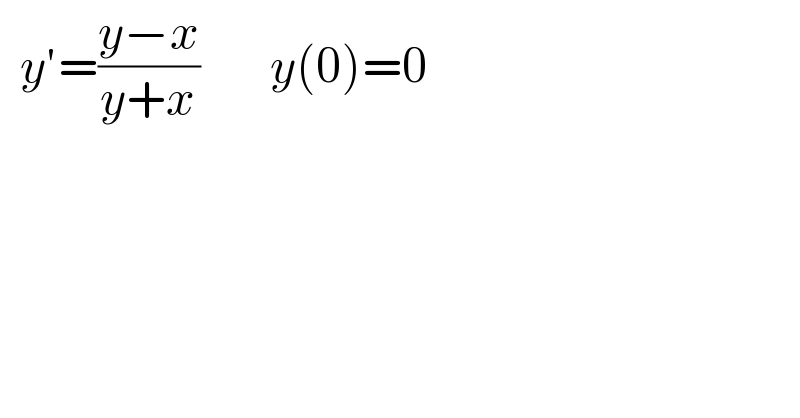
y′=((y−x)/(y+x)) y(0)=0
$$\:\:{y}'=\frac{{y}−{x}}{{y}+{x}}\:\:\:\:\:\:\:{y}\left(\mathrm{0}\right)=\mathrm{0} \\ $$
Answered by bemath last updated on 24/Jul/20
y=px ⇒ (dy/dx) = p+x(dp/dx) ⇔p+x(dp/dx) = ((x(p−1))/(x(p+1))) x(dp/dx) = ((p−1)/(p+1))−((p(p+1))/(p+1)) x(dp/dx) = ((−p^2 −1)/(p+1)) ⇒((p+1)/(p^2 +1))dp=−(dx/x) (1/2)∫((d(p^2 +1))/(p^2 +1))+∫(dp/(p^2 +1))= −lnx +C (1/2)ln (p^2 +1)+tan^(−1) (p)=−lnx+C ln (x(√(p^2 +1)))+tan^(−1) (p) = C ln ((√(y^2 +x^2 ))) + tan^(−1) ((y/x)) = C
$${y}={px}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:{p}+{x}\frac{{dp}}{{dx}} \\ $$$$\Leftrightarrow{p}+{x}\frac{{dp}}{{dx}}\:=\:\frac{{x}\left({p}−\mathrm{1}\right)}{{x}\left({p}+\mathrm{1}\right)} \\ $$$${x}\frac{{dp}}{{dx}}\:=\:\frac{{p}−\mathrm{1}}{{p}+\mathrm{1}}−\frac{{p}\left({p}+\mathrm{1}\right)}{{p}+\mathrm{1}} \\ $$$${x}\frac{{dp}}{{dx}}\:=\:\frac{−{p}^{\mathrm{2}} −\mathrm{1}}{{p}+\mathrm{1}}\:\Rightarrow\frac{{p}+\mathrm{1}}{{p}^{\mathrm{2}} +\mathrm{1}}{dp}=−\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({p}^{\mathrm{2}} +\mathrm{1}\right)}{{p}^{\mathrm{2}} +\mathrm{1}}+\int\frac{{dp}}{{p}^{\mathrm{2}} +\mathrm{1}}=\:−\mathrm{ln}{x}\:+{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({p}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{tan}^{−\mathrm{1}} \left({p}\right)=−\mathrm{ln}{x}+{C} \\ $$$$\mathrm{ln}\:\left({x}\sqrt{{p}^{\mathrm{2}} +\mathrm{1}}\right)+\mathrm{tan}^{−\mathrm{1}} \left({p}\right)\:=\:{C} \\ $$$$\mathrm{ln}\:\left(\sqrt{{y}^{\mathrm{2}} +{x}^{\mathrm{2}} }\right)\:+\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)\:=\:{C} \\ $$
Commented by 1549442205PVT last updated on 25/Jul/20
this result don′t allow us to check original condition easily
$$\mathrm{this}\:\mathrm{result}\:\mathrm{don}'\mathrm{t}\:\mathrm{allow}\:\mathrm{us}\:\mathrm{to}\:\mathrm{check} \\ $$$$\mathrm{original}\:\mathrm{condition}\:\mathrm{easily} \\ $$
Answered by ajfour last updated on 24/Jul/20
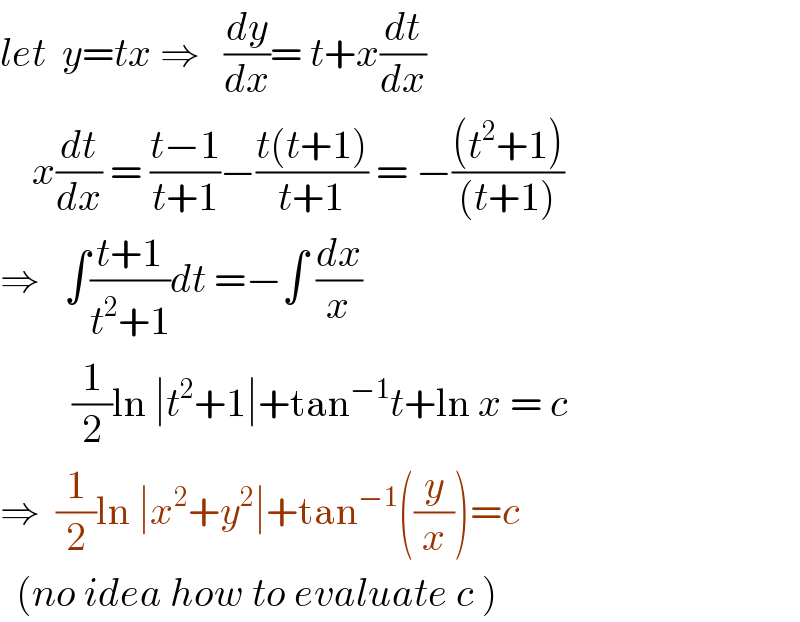
let y=tx ⇒ (dy/dx)= t+x(dt/dx) x(dt/dx) = ((t−1)/(t+1))−((t(t+1))/(t+1)) = −(((t^2 +1))/((t+1))) ⇒ ∫((t+1)/(t^2 +1))dt =−∫ (dx/x) (1/2)ln ∣t^2 +1∣+tan^(−1) t+ln x = c ⇒ (1/2)ln ∣x^2 +y^2 ∣+tan^(−1) ((y/x))=c (no idea how to evaluate c )
$${let}\:\:{y}={tx}\:\Rightarrow\:\:\:\frac{{dy}}{{dx}}=\:{t}+{x}\frac{{dt}}{{dx}} \\ $$$$\:\:\:\:{x}\frac{{dt}}{{dx}}\:=\:\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}−\frac{{t}\left({t}+\mathrm{1}\right)}{{t}+\mathrm{1}}\:=\:−\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{\left({t}+\mathrm{1}\right)} \\ $$$$\Rightarrow\:\:\:\int\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\:=−\int\:\frac{{dx}}{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{t}^{\mathrm{2}} +\mathrm{1}\mid+\mathrm{tan}^{−\mathrm{1}} {t}+\mathrm{ln}\:{x}\:=\:{c} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \mid+\mathrm{tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)={c} \\ $$$$\:\:\left({no}\:{idea}\:{how}\:{to}\:{evaluate}\:{c}\:\right)\: \\ $$
Answered by 1549442205PVT last updated on 24/Jul/20
Put x=yt⇒dx=ydt+tdy⇒(dy/dx)=((y−x)/(y+x))=((1−t)/(t+1)) ((ydt+tdy)/dy)=((1+t)/(1−t))⇒((ydt)/dy)=((1−t^2 )/(1−t))⇒(dy/y)=((1−t)/(1−t^2 ))dt (dy/y)=(dt/(1+t))⇒ln∣y∣=ln∣1+t∣+lnC(C>0) ⇒y=C(1+t)=C(1+(x/y)) ⇔y^2 =C(x+y)⇔y^2 −Cy−Cx=0 𝚫=C^2 +4Cx⇒y=((C+(√(C^2 +4Cx)))/2) or y=((C−(√(C^2 +4Cx)))/2) i)If y=((C+(√(C^2 +4Cx)))/2) then y(0)=0⇒0=((C+C)/2)⇔C=0⇒y≡0 contradiction. ii)If y=((C−(√(C^2 +4Cx)))/2) then y(0)=0⇔0=((C−C)/2) is true ∀C>0 Thus ,y=((C−(√(C^2 +4Cx)))/2)
$$\mathrm{Put}\:\mathrm{x}=\mathrm{yt}\Rightarrow\mathrm{dx}=\mathrm{ydt}+\mathrm{tdy}\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{y}−\mathrm{x}}{\mathrm{y}+\mathrm{x}}=\frac{\mathrm{1}−\mathrm{t}}{\mathrm{t}+\mathrm{1}} \\ $$$$\frac{\mathrm{ydt}+\mathrm{tdy}}{\mathrm{dy}}=\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}\Rightarrow\frac{\mathrm{ydt}}{\mathrm{dy}}=\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}−\mathrm{t}}\Rightarrow\frac{\mathrm{dy}}{\mathrm{y}}=\frac{\mathrm{1}−\mathrm{t}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\frac{\mathrm{dy}}{\mathrm{y}}=\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}}\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid=\mathrm{ln}\mid\mathrm{1}+\mathrm{t}\mid+\mathrm{lnC}\left(\mathrm{C}>\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{y}=\mathrm{C}\left(\mathrm{1}+\mathrm{t}\right)=\mathrm{C}\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{y}}\right) \\ $$$$\Leftrightarrow\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\boldsymbol{\mathrm{C}}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)\Leftrightarrow\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\boldsymbol{\mathrm{Cy}}−\boldsymbol{\mathrm{Cx}}=\mathrm{0} \\ $$$$\boldsymbol{\Delta}=\boldsymbol{\mathrm{C}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{\mathrm{Cx}}\Rightarrow\boldsymbol{\mathrm{y}}=\frac{\boldsymbol{\mathrm{C}}+\sqrt{\boldsymbol{\mathrm{C}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{\mathrm{Cx}}}}{\mathrm{2}}\: \\ $$$$\boldsymbol{\mathrm{or}}\:\boldsymbol{\mathrm{y}}=\frac{\boldsymbol{\mathrm{C}}−\sqrt{\boldsymbol{\mathrm{C}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{\mathrm{Cx}}}}{\mathrm{2}} \\ $$$$\left.\boldsymbol{\mathrm{i}}\right)\boldsymbol{\mathrm{I}}\mathrm{f}\:\boldsymbol{\mathrm{y}}=\frac{\boldsymbol{\mathrm{C}}+\sqrt{\boldsymbol{\mathrm{C}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{\mathrm{Cx}}}}{\mathrm{2}}\:\:\boldsymbol{\mathrm{then}} \\ $$$$\boldsymbol{\mathrm{y}}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow\mathrm{0}=\frac{\boldsymbol{\mathrm{C}}+\boldsymbol{\mathrm{C}}}{\mathrm{2}}\Leftrightarrow\boldsymbol{\mathrm{C}}=\mathrm{0}\Rightarrow\boldsymbol{\mathrm{y}}\equiv\mathrm{0} \\ $$$$\boldsymbol{\mathrm{contradiction}}. \\ $$$$\left.\boldsymbol{\mathrm{ii}}\right)\boldsymbol{\mathrm{If}}\:\boldsymbol{\mathrm{y}}=\frac{\boldsymbol{\mathrm{C}}−\sqrt{\boldsymbol{\mathrm{C}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{\mathrm{Cx}}}}{\mathrm{2}}\:\:\boldsymbol{\mathrm{then}}\: \\ $$$$\boldsymbol{\mathrm{y}}\left(\mathrm{0}\right)=\mathrm{0}\Leftrightarrow\mathrm{0}=\frac{\boldsymbol{\mathrm{C}}−\boldsymbol{\mathrm{C}}}{\mathrm{2}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{true}}\:\forall\boldsymbol{\mathrm{C}}>\mathrm{0} \\ $$$$\boldsymbol{\mathrm{Thus}}\:,\boldsymbol{\mathrm{y}}=\frac{\boldsymbol{\mathrm{C}}−\sqrt{\boldsymbol{\mathrm{C}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{\mathrm{Cx}}}}{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *