Question Number 100184 by bobhans last updated on 25/Jun/20
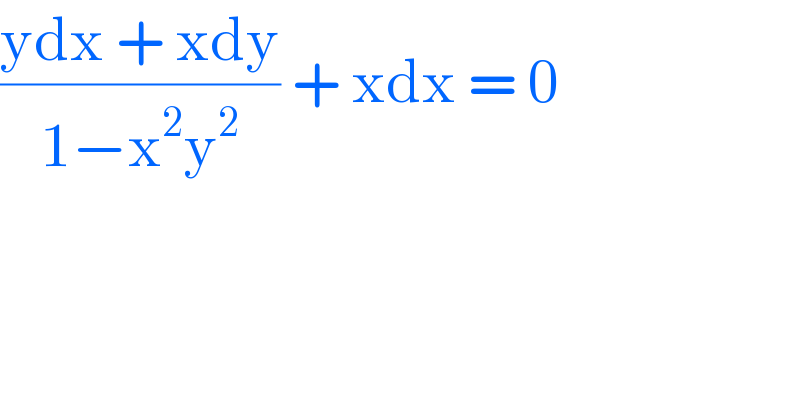
$$\frac{\mathrm{ydx}\:+\:\mathrm{xdy}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} }\:+\:\mathrm{xdx}\:=\:\mathrm{0} \\ $$
Answered by maths mind last updated on 26/Jun/20
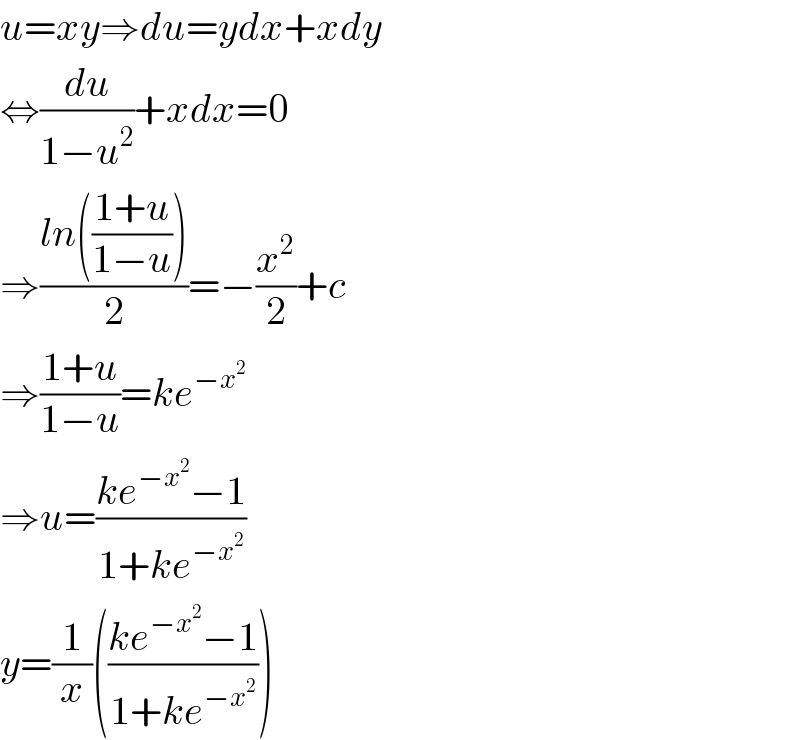
$${u}={xy}\Rightarrow{du}={ydx}+{xdy} \\ $$$$\Leftrightarrow\frac{{du}}{\mathrm{1}−{u}^{\mathrm{2}} }+{xdx}=\mathrm{0} \\ $$$$\Rightarrow\frac{{ln}\left(\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\right)}{\mathrm{2}}=−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{c} \\ $$$$\Rightarrow\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}={ke}^{−{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{u}=\frac{{ke}^{−{x}^{\mathrm{2}} } −\mathrm{1}}{\mathrm{1}+{ke}^{−{x}^{\mathrm{2}} } } \\ $$$${y}=\frac{\mathrm{1}}{{x}}\left(\frac{{ke}^{−{x}^{\mathrm{2}} } −\mathrm{1}}{\mathrm{1}+{ke}^{−{x}^{\mathrm{2}} } }\right) \\ $$
