Question Number 128106 by bemath last updated on 04/Jan/21
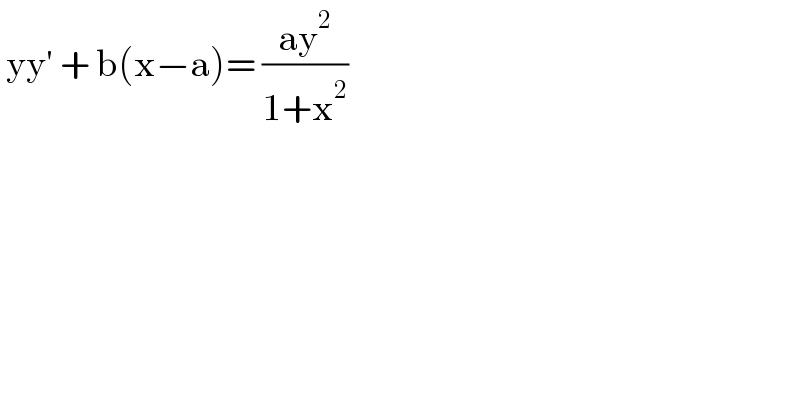
$$\:\mathrm{yy}'\:+\:\mathrm{b}\left(\mathrm{x}−\mathrm{a}\right)=\:\frac{\mathrm{ay}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\: \\ $$
Commented by mr W last updated on 05/Jan/21

$${once}\:{i}\:{asked}\:{this}\:{question}\:{due}\:{to} \\ $$$${Q}\mathrm{127997},\:{but}\:{then}\:{i}\:{could}\:{solve}\:{it}\:{myself} \\ $$$${and}\:{therefore}\:{have}\:{deleted}\:{the}\:{post}. \\ $$$${my}\:{post}\:{existed}\:{only}\:{for}\:{a}\:{short}\:{time}. \\ $$$${thank}\:{you}\:{that}\:{you}\:{have}\:{noticed}\:{my}\: \\ $$$${post}\:{nevertheless}\:{and}\:{restored}\:{the} \\ $$$${question}\:{here}! \\ $$$${i}\:{enjoyed}\:{that}\:{i}\:{could}\:{solve} \\ $$$${Q}\mathrm{127997}\:{completely}.\:{please}\:{check}\:{out} \\ $$$${the}\:{solution}\:{there},\:{comments}\:{are} \\ $$$${welcome}! \\ $$
Answered by liberty last updated on 04/Jan/21

$$\:\mathrm{yy}'+\mathrm{b}\left(\mathrm{x}−\mathrm{a}\right)=\frac{\mathrm{ay}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{yy}'−\frac{\mathrm{ay}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{b}\left(\mathrm{a}−\mathrm{x}\right) \\ $$$$\:\mathrm{let}\:\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{v}\:\Rightarrow\mathrm{2yy}'\:=\:\mathrm{v}'\:;\:\mathrm{yy}'\:=\:\frac{\mathrm{v}'}{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{v}'}{\mathrm{2}}−\frac{\mathrm{a}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }.\mathrm{v}\:=\:\mathrm{b}\left(\mathrm{a}−\mathrm{x}\right)\:;\:\mathrm{v}'−\frac{\mathrm{2a}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }.\mathrm{v}=\mathrm{2b}\left(\mathrm{a}−\mathrm{x}\right) \\ $$$$\mathrm{put}\:\mathrm{IF}\:\mu\:=\:\mathrm{e}^{−\int\:\frac{\mathrm{2a}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}} =\:\mathrm{e}^{−\mathrm{2a}\:.\mathrm{arctan}\:\mathrm{x}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{v}\:=\:\frac{\int\mathrm{2b}\left(\mathrm{a}−\mathrm{x}\right)\mathrm{e}^{−\mathrm{2a}.\mathrm{arctan}\:\mathrm{x}} \:\mathrm{dx}+\mathrm{C}}{\mathrm{e}^{−\mathrm{2}.\mathrm{arctan}\:\mathrm{x}} } \\ $$$$\:\therefore\:\mathrm{y}^{\mathrm{2}} =\:\mathrm{C}.\mathrm{e}^{\mathrm{2a}.\mathrm{arctan}\:\mathrm{x}} \:+\:\mathrm{2b}\int\:\left(\mathrm{a}−\mathrm{x}\right).\mathrm{e}^{−\mathrm{2a}.\mathrm{arctan}\:\mathrm{x}} \:\mathrm{dx}\: \\ $$
Commented by mr W last updated on 05/Jan/21

$${for}\:{complete}\:{solution}\:{see}\:{Q}\mathrm{127997}. \\ $$
