Question Number 127610 by pticantor last updated on 31/Dec/20
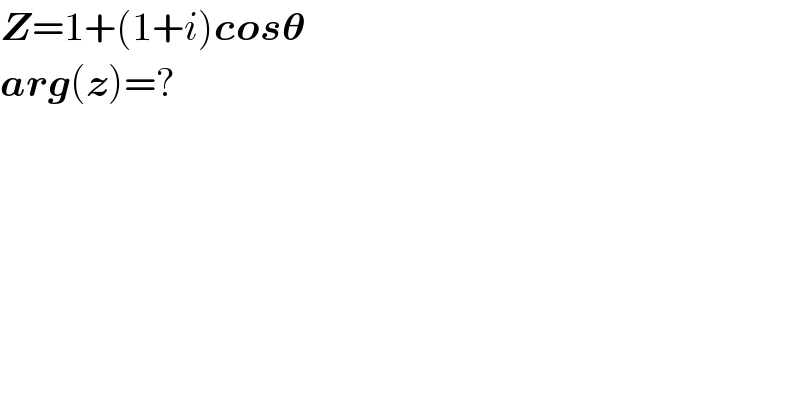
$$\boldsymbol{{Z}}=\mathrm{1}+\left(\mathrm{1}+{i}\right)\boldsymbol{{cos}\theta} \\ $$$$\boldsymbol{{arg}}\left(\boldsymbol{{z}}\right)=? \\ $$
Answered by MJS_new last updated on 31/Dec/20
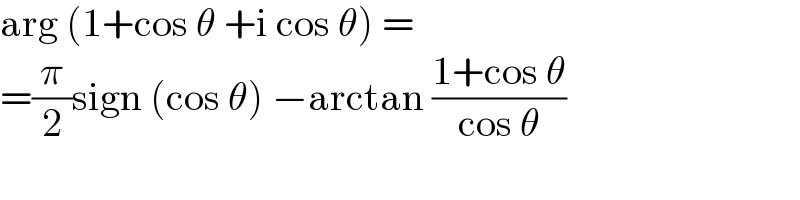
$$\mathrm{arg}\:\left(\mathrm{1}+\mathrm{cos}\:\theta\:+\mathrm{i}\:\mathrm{cos}\:\theta\right)\:= \\ $$$$=\frac{\pi}{\mathrm{2}}\mathrm{sign}\:\left(\mathrm{cos}\:\theta\right)\:−\mathrm{arctan}\:\frac{\mathrm{1}+\mathrm{cos}\:\theta}{\mathrm{cos}\:\theta} \\ $$
Commented by pticantor last updated on 31/Dec/20
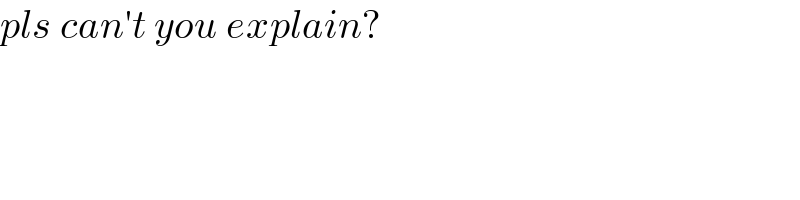
$${pls}\:{can}'{t}\:{you}\:{explain}? \\ $$
Commented by MJS_new last updated on 31/Dec/20

$$\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{the}\:\mathrm{formula} \\ $$$$\mathrm{arg}\:\left({a}+{b}\mathrm{i}\right)\:=\frac{\pi}{\mathrm{2}}\mathrm{sign}\:{b}\:−\mathrm{arctan}\:\frac{{a}}{{b}} \\ $$$$\mathrm{which}\:\mathrm{gives}\:\mathrm{an}\:\mathrm{angle}\:\varphi\:\mathrm{with}\:−\pi\leqslant\varphi<\pi \\ $$$$\mathrm{test}\:\mathrm{it}\:\mathrm{for}\:{z}={a}+{b}\mathrm{i}\:\mathrm{in}\:\mathrm{all}\:\mathrm{4}\:\mathrm{quadrants}: \\ $$$${z}=\begin{cases}{+\mathrm{1}}\\{−\mathrm{1}}\\{−\mathrm{1}}\\{+\mathrm{1}}\end{cases}\:\left.\begin{matrix}{+\mathrm{i}}\\{+\mathrm{i}}\\{−\mathrm{i}}\\{−\mathrm{i}}\end{matrix}\right\}\:\Rightarrow\:\mathrm{arg}\:{z}\:=\begin{cases}{\pi/\mathrm{2}−\mathrm{arctan}\:\mathrm{1}\:=\pi/\mathrm{4}}\\{\pi/\mathrm{2}−\mathrm{arctan}\:\left(−\mathrm{1}\right)\:=\mathrm{3}\pi/\mathrm{4}}\\{−\pi/\mathrm{2}−\mathrm{arctan}\:\mathrm{1}\:=−\mathrm{3}\pi/\mathrm{4}}\\{−\pi/\mathrm{2}−\mathrm{arctan}\:\left(−\mathrm{1}\right)\:=−\pi/\mathrm{4}}\end{cases} \\ $$
Answered by mathmax by abdo last updated on 01/Jan/21
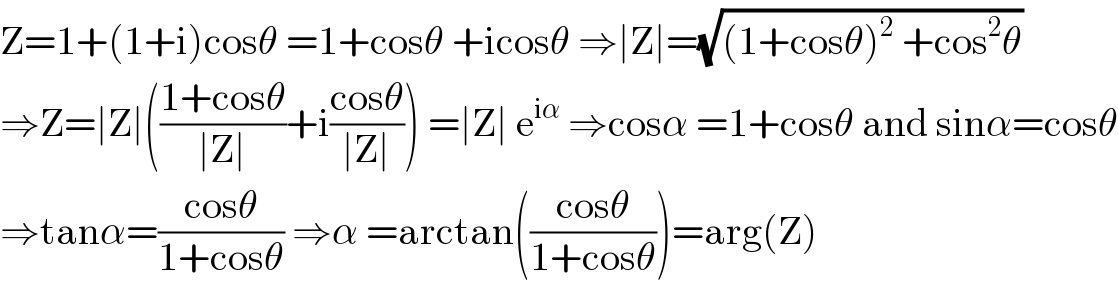
$$\mathrm{Z}=\mathrm{1}+\left(\mathrm{1}+\mathrm{i}\right)\mathrm{cos}\theta\:=\mathrm{1}+\mathrm{cos}\theta\:+\mathrm{icos}\theta\:\Rightarrow\mid\mathrm{Z}\mid=\sqrt{\left(\mathrm{1}+\mathrm{cos}\theta\right)^{\mathrm{2}} \:+\mathrm{cos}^{\mathrm{2}} \theta} \\ $$$$\Rightarrow\mathrm{Z}=\mid\mathrm{Z}\mid\left(\frac{\mathrm{1}+\mathrm{cos}\theta}{\mid\mathrm{Z}\mid}+\mathrm{i}\frac{\mathrm{cos}\theta}{\mid\mathrm{Z}\mid}\right)\:=\mid\mathrm{Z}\mid\:\mathrm{e}^{\mathrm{i}\alpha} \:\Rightarrow\mathrm{cos}\alpha\:=\mathrm{1}+\mathrm{cos}\theta\:\mathrm{and}\:\mathrm{sin}\alpha=\mathrm{cos}\theta \\ $$$$\Rightarrow\mathrm{tan}\alpha=\frac{\mathrm{cos}\theta}{\mathrm{1}+\mathrm{cos}\theta}\:\Rightarrow\alpha\:=\mathrm{arctan}\left(\frac{\mathrm{cos}\theta}{\mathrm{1}+\mathrm{cos}\theta}\right)=\mathrm{arg}\left(\mathrm{Z}\right) \\ $$
