Menu Close

z-1-3-i-z-2-1-2i-determinant-2z-2-z-1-5-i-2z-1-z-2-3-i-2-

Tinku Tara 0 Comments
Pin




Question Number 47391 by gunawan last updated on 09/Nov/18
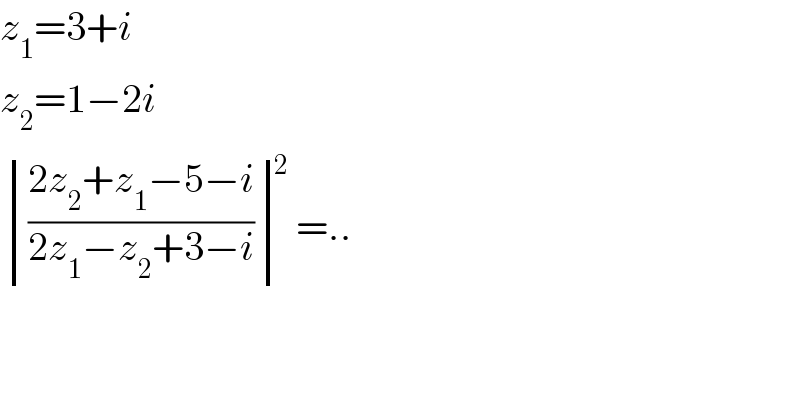
z_1 =3+i z_2 =1−2i determinant ((((2z_2 +z_1 −5−i)/(2z_1 −z_2 +3−i))))^2 =..
$${z}_{\mathrm{1}} =\mathrm{3}+{i} \\ $$$${z}_{\mathrm{2}} =\mathrm{1}−\mathrm{2}{i} \\ $$$$\begin{vmatrix}{\frac{\mathrm{2}{z}_{\mathrm{2}} +{z}_{\mathrm{1}} −\mathrm{5}−{i}}{\mathrm{2}{z}_{\mathrm{1}} −{z}_{\mathrm{2}} +\mathrm{3}−{i}}}\end{vmatrix}^{\mathrm{2}} =.. \\ $$
Commented by maxmathsup by imad last updated on 10/Nov/18
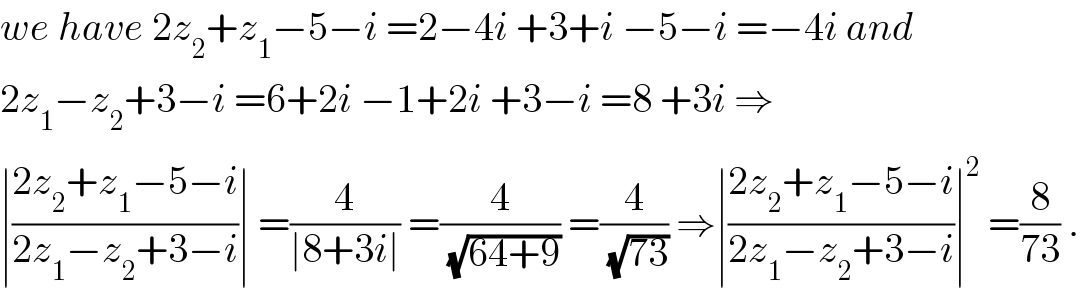
we have 2z_2 +z_1 −5−i =2−4i +3+i −5−i =−4i and 2z_1 −z_2 +3−i =6+2i −1+2i +3−i =8 +3i ⇒ ∣((2z_2 +z_1 −5−i)/(2z_1 −z_2 +3−i))∣ =(4/(∣8+3i∣)) =(4/( (√(64+9)))) =(4/( (√(73)))) ⇒∣((2z_2 +z_1 −5−i)/(2z_1 −z_2 +3−i))∣^2 =(8/(73)) .
$${we}\:{have}\:\mathrm{2}{z}_{\mathrm{2}} +{z}_{\mathrm{1}} −\mathrm{5}−{i}\:=\mathrm{2}−\mathrm{4}{i}\:+\mathrm{3}+{i}\:−\mathrm{5}−{i}\:=−\mathrm{4}{i}\:{and}\: \\ $$$$\mathrm{2}{z}_{\mathrm{1}} −{z}_{\mathrm{2}} +\mathrm{3}−{i}\:=\mathrm{6}+\mathrm{2}{i}\:−\mathrm{1}+\mathrm{2}{i}\:+\mathrm{3}−{i}\:=\mathrm{8}\:+\mathrm{3}{i}\:\Rightarrow \\ $$$$\mid\frac{\mathrm{2}{z}_{\mathrm{2}} +{z}_{\mathrm{1}} −\mathrm{5}−{i}}{\mathrm{2}{z}_{\mathrm{1}} −{z}_{\mathrm{2}} +\mathrm{3}−{i}}\mid\:=\frac{\mathrm{4}}{\mid\mathrm{8}+\mathrm{3}{i}\mid}\:=\frac{\mathrm{4}}{\:\sqrt{\mathrm{64}+\mathrm{9}}}\:=\frac{\mathrm{4}}{\:\sqrt{\mathrm{73}}}\:\Rightarrow\mid\frac{\mathrm{2}{z}_{\mathrm{2}} +{z}_{\mathrm{1}} −\mathrm{5}−{i}}{\mathrm{2}{z}_{\mathrm{1}} −{z}_{\mathrm{2}} +\mathrm{3}−{i}}\mid^{\mathrm{2}} \:=\frac{\mathrm{8}}{\mathrm{73}}\:. \\ $$
Answered by mr W last updated on 11/Nov/18
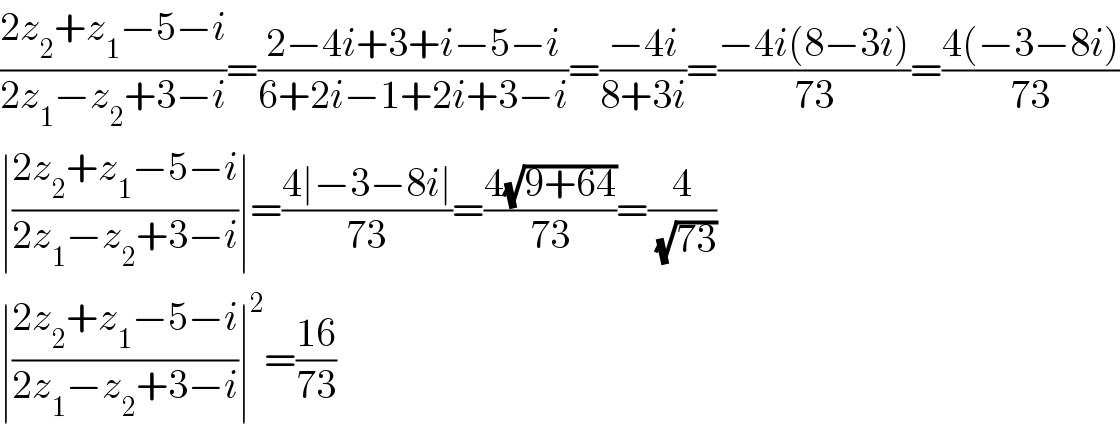
((2z_2 +z_1 −5−i)/(2z_1 −z_2 +3−i))=((2−4i+3+i−5−i)/(6+2i−1+2i+3−i))=((−4i)/(8+3i))=((−4i(8−3i))/(73))=((4(−3−8i))/(73)) ∣((2z_2 +z_1 −5−i)/(2z_1 −z_2 +3−i))∣=((4∣−3−8i∣)/(73))=((4(√(9+64)))/(73))=(4/( (√(73)))) ∣((2z_2 +z_1 −5−i)/(2z_1 −z_2 +3−i))∣^2 =((16)/(73))
$$\frac{\mathrm{2}{z}_{\mathrm{2}} +{z}_{\mathrm{1}} −\mathrm{5}−{i}}{\mathrm{2}{z}_{\mathrm{1}} −{z}_{\mathrm{2}} +\mathrm{3}−{i}}=\frac{\mathrm{2}−\mathrm{4}{i}+\mathrm{3}+{i}−\mathrm{5}−{i}}{\mathrm{6}+\mathrm{2}{i}−\mathrm{1}+\mathrm{2}{i}+\mathrm{3}−{i}}=\frac{−\mathrm{4}{i}}{\mathrm{8}+\mathrm{3}{i}}=\frac{−\mathrm{4}{i}\left(\mathrm{8}−\mathrm{3}{i}\right)}{\mathrm{73}}=\frac{\mathrm{4}\left(−\mathrm{3}−\mathrm{8}{i}\right)}{\mathrm{73}} \\ $$$$\mid\frac{\mathrm{2}{z}_{\mathrm{2}} +{z}_{\mathrm{1}} −\mathrm{5}−{i}}{\mathrm{2}{z}_{\mathrm{1}} −{z}_{\mathrm{2}} +\mathrm{3}−{i}}\mid=\frac{\mathrm{4}\mid−\mathrm{3}−\mathrm{8}{i}\mid}{\mathrm{73}}=\frac{\mathrm{4}\sqrt{\mathrm{9}+\mathrm{64}}}{\mathrm{73}}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{73}}} \\ $$$$\mid\frac{\mathrm{2}{z}_{\mathrm{2}} +{z}_{\mathrm{1}} −\mathrm{5}−{i}}{\mathrm{2}{z}_{\mathrm{1}} −{z}_{\mathrm{2}} +\mathrm{3}−{i}}\mid^{\mathrm{2}} =\frac{\mathrm{16}}{\mathrm{73}} \\ $$
Answered by ajfour last updated on 10/Nov/18
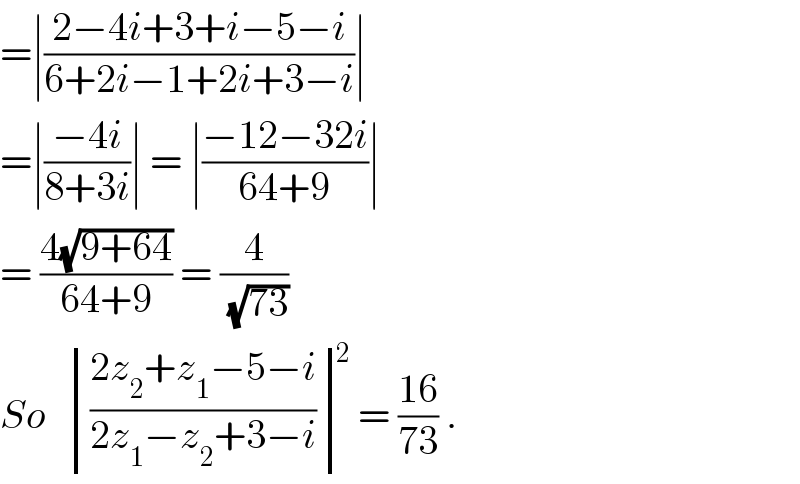
=∣((2−4i+3+i−5−i)/(6+2i−1+2i+3−i))∣ =∣((−4i)/(8+3i))∣ = ∣((−12−32i)/(64+9))∣ = ((4(√(9+64)))/(64+9)) = (4/( (√(73)))) So determinant ((((2z_2 +z_1 −5−i)/(2z_1 −z_2 +3−i))))^2 = ((16)/(73)) .
$$=\mid\frac{\mathrm{2}−\mathrm{4}{i}+\mathrm{3}+{i}−\mathrm{5}−{i}}{\mathrm{6}+\mathrm{2}{i}−\mathrm{1}+\mathrm{2}{i}+\mathrm{3}−{i}}\mid \\ $$$$=\mid\frac{−\mathrm{4}{i}}{\mathrm{8}+\mathrm{3}{i}}\mid\:=\:\mid\frac{−\mathrm{12}−\mathrm{32}{i}}{\mathrm{64}+\mathrm{9}}\mid \\ $$$$=\:\frac{\mathrm{4}\sqrt{\mathrm{9}+\mathrm{64}}}{\mathrm{64}+\mathrm{9}}\:=\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{73}}} \\ $$$${So}\:\:\begin{vmatrix}{\frac{\mathrm{2}{z}_{\mathrm{2}} +{z}_{\mathrm{1}} −\mathrm{5}−{i}}{\mathrm{2}{z}_{\mathrm{1}} −{z}_{\mathrm{2}} +\mathrm{3}−{i}}}\end{vmatrix}^{\mathrm{2}} =\:\frac{\mathrm{16}}{\mathrm{73}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *