Question Number 124320 by sogol last updated on 02/Dec/20

$${z}+\frac{\mathrm{1}}{{z}}=\mathrm{1} \\ $$$${z}^{\mathrm{3}} =?? \\ $$
Answered by Dwaipayan Shikari last updated on 02/Dec/20
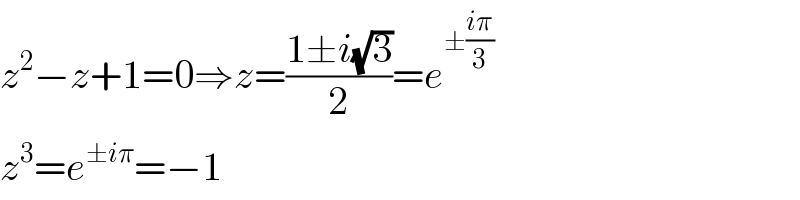
$${z}^{\mathrm{2}} −{z}+\mathrm{1}=\mathrm{0}\Rightarrow{z}=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{\pm\frac{{i}\pi}{\mathrm{3}}} \\ $$$${z}^{\mathrm{3}} ={e}^{\pm{i}\pi} =−\mathrm{1} \\ $$
Answered by $@y@m last updated on 02/Dec/20
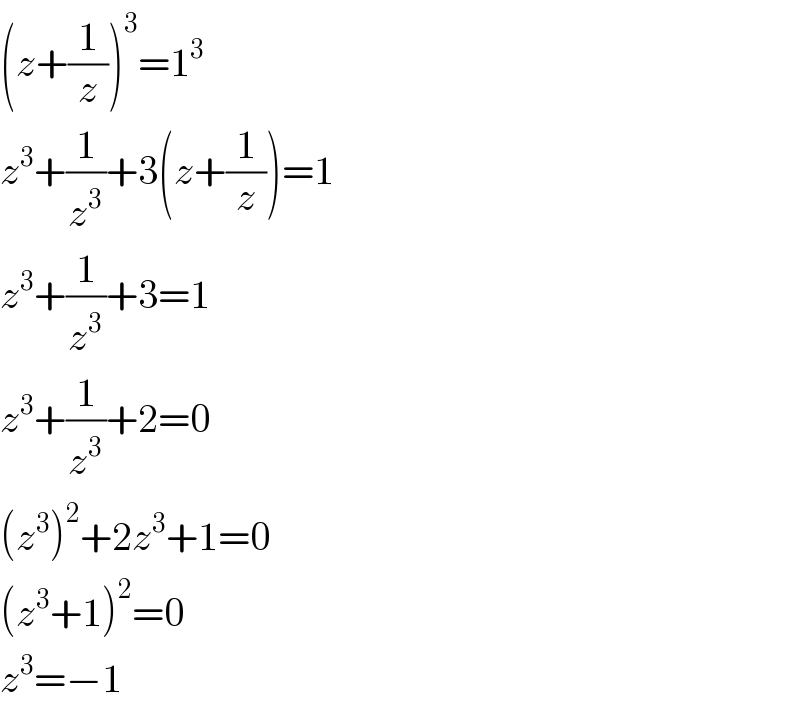
$$\left({z}+\frac{\mathrm{1}}{{z}}\right)^{\mathrm{3}} =\mathrm{1}^{\mathrm{3}} \\ $$$${z}^{\mathrm{3}} +\frac{\mathrm{1}}{{z}^{\mathrm{3}} }+\mathrm{3}\left({z}+\frac{\mathrm{1}}{{z}}\right)=\mathrm{1} \\ $$$${z}^{\mathrm{3}} +\frac{\mathrm{1}}{{z}^{\mathrm{3}} }+\mathrm{3}=\mathrm{1} \\ $$$${z}^{\mathrm{3}} +\frac{\mathrm{1}}{{z}^{\mathrm{3}} }+\mathrm{2}=\mathrm{0} \\ $$$$\left({z}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{2}{z}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$$\left({z}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${z}^{\mathrm{3}} =−\mathrm{1} \\ $$
