Question Number 118780 by mathocean1 last updated on 19/Oct/20
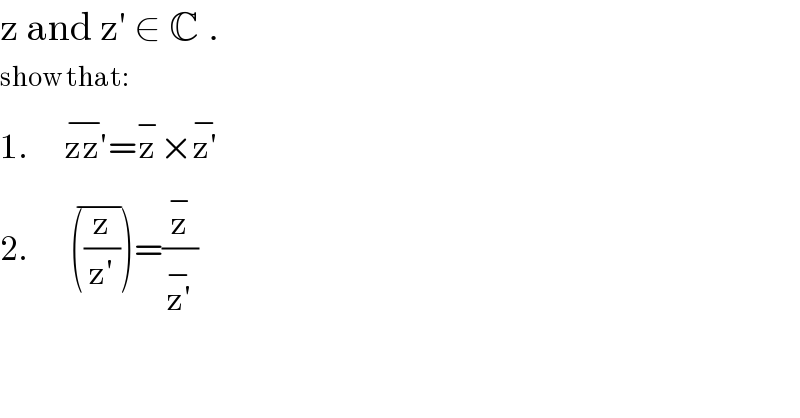
$$\mathrm{z}\:\mathrm{and}\:\mathrm{z}'\:\in\:\mathbb{C}\:. \\ $$$$\mathrm{show}\:\mathrm{that}: \\ $$$$\mathrm{1}.\:\:\:\:\:\:\overline {\mathrm{zz}'}=\overset{−} {\mathrm{z}}×\overline {\mathrm{z}'} \\ $$$$\mathrm{2}.\:\:\:\:\:\:\:\overline {\left(\frac{\mathrm{z}}{\mathrm{z}'}\right)}=\frac{\overset{−} {\mathrm{z}}}{\overline {\mathrm{z}'}} \\ $$$$ \\ $$
Answered by MJS_new last updated on 19/Oct/20
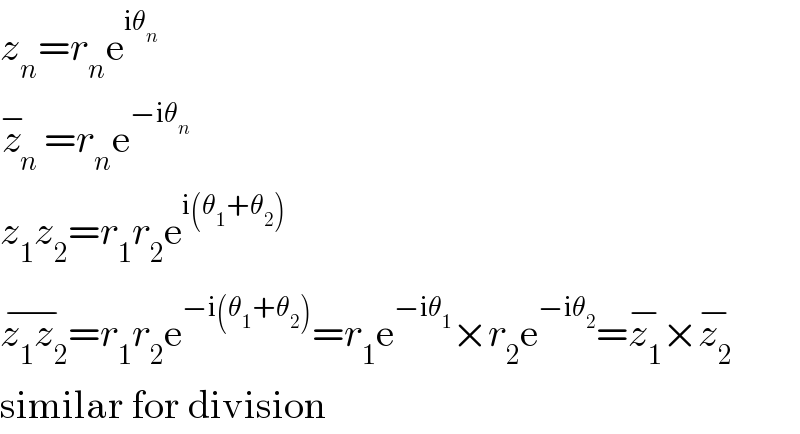
$${z}_{{n}} ={r}_{{n}} \mathrm{e}^{\mathrm{i}\theta_{{n}} } \\ $$$$\overset{−} {{z}}_{{n}} ={r}_{{n}} \mathrm{e}^{−\mathrm{i}\theta_{{n}} } \\ $$$${z}_{\mathrm{1}} {z}_{\mathrm{2}} ={r}_{\mathrm{1}} {r}_{\mathrm{2}} \mathrm{e}^{\mathrm{i}\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)} \\ $$$$\overline {{z}_{\mathrm{1}} {z}_{\mathrm{2}} }={r}_{\mathrm{1}} {r}_{\mathrm{2}} \mathrm{e}^{−\mathrm{i}\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)} ={r}_{\mathrm{1}} \mathrm{e}^{−\mathrm{i}\theta_{\mathrm{1}} } ×{r}_{\mathrm{2}} \mathrm{e}^{−\mathrm{i}\theta_{\mathrm{2}} } =\overline {{z}_{\mathrm{1}} }×\overline {{z}_{\mathrm{2}} } \\ $$$$\mathrm{similar}\:\mathrm{for}\:\mathrm{division} \\ $$
Commented by mathocean1 last updated on 19/Oct/20

$$\mathrm{thanks} \\ $$$$ \\ $$$$ \\ $$
Answered by Olaf last updated on 19/Oct/20

$${z}\:=\:{a}+{ib}\:\mathrm{and}\:{z}'\:=\:{a}'+{ib}' \\ $$$$\overset{\_} {{z}}\:=\:{a}−{ib}\:\mathrm{and}\:\overset{\_} {{z}'}\:=\:{a}'−{ib}' \\ $$$$ \\ $$$${zz}'\:=\:{aa}'−{bb}'+\left({ab}'+{a}'{b}\right){i} \\ $$$$\overset{\_\_} {{zz}'}\:=\:{aa}'−{bb}'−\left({ab}'+{a}'{b}\right){i}\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\overset{\_} {{z}}\overset{\_} {{z}'}\:=\:\left({a}−{ib}\right)\left({a}'−{ib}'\right) \\ $$$$\overset{\_} {{z}}\overset{\_} {{z}'}\:=\:{aa}'−{bb}'−\left({ab}'+{a}'{b}\right)\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{With}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\::\:\overset{\_\_} {{zz}'}\:=\:\overset{\_} {{z}}\overset{\_} {{z}'} \\ $$$$ \\ $$$$\mathrm{Same}\:\mathrm{reasoning}\:\mathrm{for}\:\mathrm{question}\:\mathrm{2}. \\ $$
