Menu Close

z-gt-0-z-2-12-z-5-z-2-z-

Tinku Tara 0 Comments
Pin




Question Number 149354 by mathdanisur last updated on 04/Aug/21
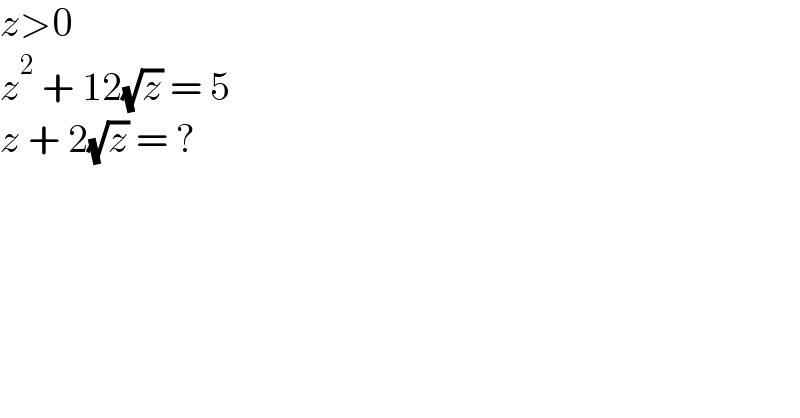
z>0 z^2 + 12(√z) = 5 z + 2(√z) = ?
$${z}>\mathrm{0} \\ $$$${z}^{\mathrm{2}} \:+\:\mathrm{12}\sqrt{{z}}\:=\:\mathrm{5} \\ $$$${z}\:+\:\mathrm{2}\sqrt{{z}}\:=\:? \\ $$
Commented by Rasheed.Sindhi last updated on 05/Aug/21
⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢⌣ GOOD Saying: “If you know nothing you must believe everything.” ⌢⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢
$$\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile \\ $$$$\mathcal{GOOD}\:\:\mathcal{S}{aying}: \\ $$$$“\mathrm{If}\:\mathrm{you}\:\mathrm{know}\:\mathrm{nothing}\:\mathrm{you}\:\mathrm{must}\:\mathrm{believe} \\ $$$$\mathrm{everything}.'' \\ $$$$\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown \\ $$
Commented by liberty last updated on 05/Aug/21
(√z) = u⇒u^4 −12u−5=0 (u^2 +bu+5)(u^2 +au−1)=0 u^4 +au^3 −u^2 +bu^3 +abu^2 −bu+5u^2 +5au−5=0 u^4 +(a+b)u^3 +(ab+4)u^2 +(5a−b)u−5=0 a=−b ; 4=a^2 → { ((a=−2)),((b=2)) :} ⇔z^2 +12z−5=0 (z+2(√z)+5)(z−2(√z)−1)=0 { ((z+2(√z) =−5)),((z−2(√z) =1 )) :}
$$\sqrt{\mathrm{z}}\:=\:\mathrm{u}\Rightarrow\mathrm{u}^{\mathrm{4}} −\mathrm{12u}−\mathrm{5}=\mathrm{0} \\ $$$$\left(\mathrm{u}^{\mathrm{2}} +\mathrm{bu}+\mathrm{5}\right)\left(\mathrm{u}^{\mathrm{2}} +\mathrm{au}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{u}^{\mathrm{4}} +\mathrm{au}^{\mathrm{3}} −\mathrm{u}^{\mathrm{2}} +\mathrm{bu}^{\mathrm{3}} +\mathrm{abu}^{\mathrm{2}} −\mathrm{bu}+\mathrm{5u}^{\mathrm{2}} +\mathrm{5au}−\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{u}^{\mathrm{4}} +\left(\mathrm{a}+\mathrm{b}\right)\mathrm{u}^{\mathrm{3}} +\left(\mathrm{ab}+\mathrm{4}\right)\mathrm{u}^{\mathrm{2}} +\left(\mathrm{5a}−\mathrm{b}\right)\mathrm{u}−\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{a}=−\mathrm{b}\:;\:\mathrm{4}=\mathrm{a}^{\mathrm{2}} \:\rightarrow\begin{cases}{\mathrm{a}=−\mathrm{2}}\\{\mathrm{b}=\mathrm{2}}\end{cases} \\ $$$$\Leftrightarrow\mathrm{z}^{\mathrm{2}} +\mathrm{12z}−\mathrm{5}=\mathrm{0} \\ $$$$\left(\mathrm{z}+\mathrm{2}\sqrt{\mathrm{z}}+\mathrm{5}\right)\left(\mathrm{z}−\mathrm{2}\sqrt{\mathrm{z}}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{z}+\mathrm{2}\sqrt{\mathrm{z}}\:=−\mathrm{5}}\\{\mathrm{z}−\mathrm{2}\sqrt{\mathrm{z}}\:=\mathrm{1}\:}\end{cases} \\ $$
Commented by mathdanisur last updated on 05/Aug/21
Thank You Ser
$${Thank}\:{You}\:{Ser} \\ $$
Commented by MJS_new last updated on 05/Aug/21
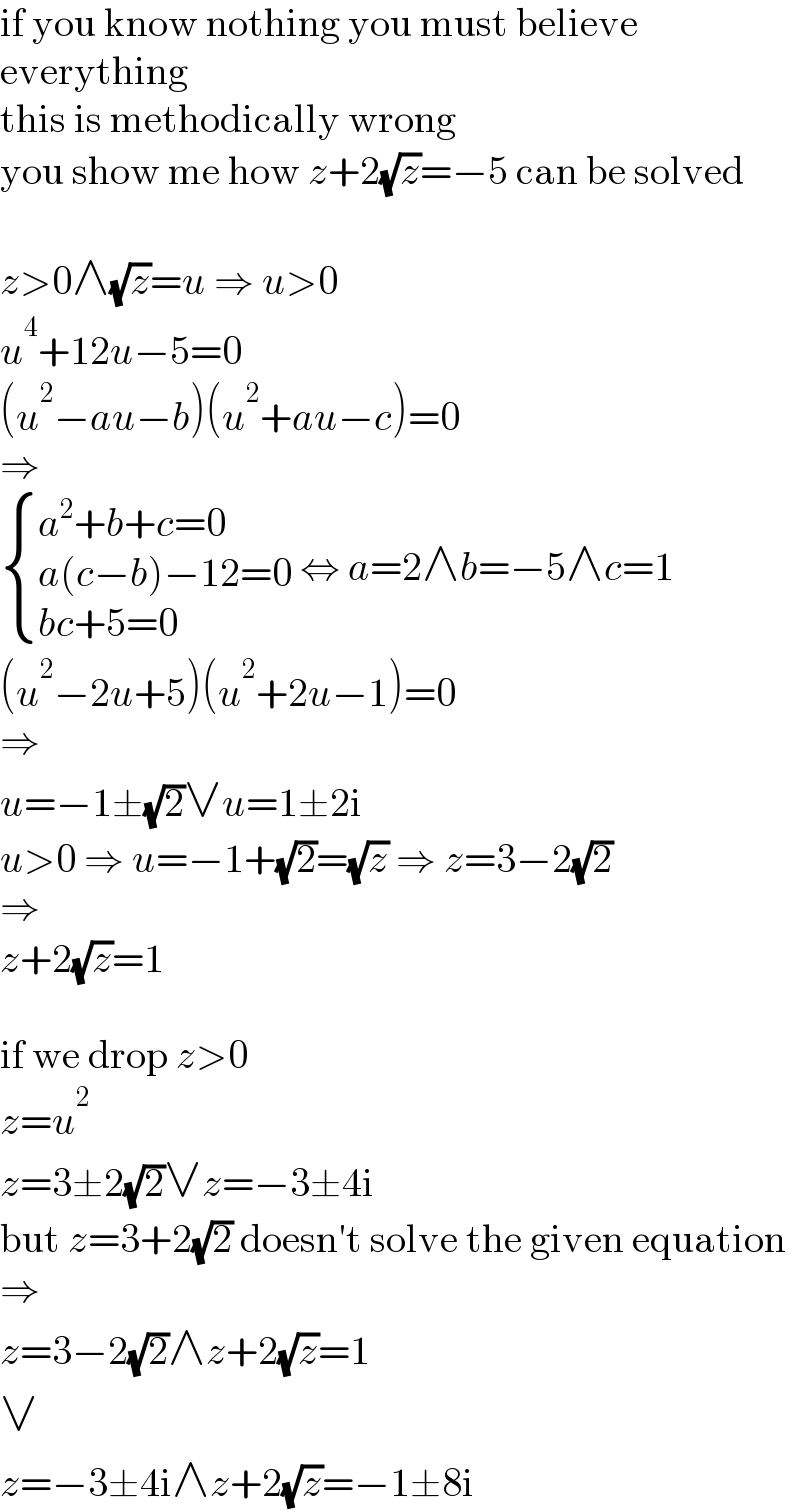
if you know nothing you must believe everything this is methodically wrong you show me how z+2(√z)=−5 can be solved z>0∧(√z)=u ⇒ u>0 u^4 +12u−5=0 (u^2 −au−b)(u^2 +au−c)=0 ⇒ { ((a^2 +b+c=0)),((a(c−b)−12=0)),((bc+5=0)) :} ⇔ a=2∧b=−5∧c=1 (u^2 −2u+5)(u^2 +2u−1)=0 ⇒ u=−1±(√2)∨u=1±2i u>0 ⇒ u=−1+(√2)=(√z) ⇒ z=3−2(√2) ⇒ z+2(√z)=1 if we drop z>0 z=u^2 z=3±2(√2)∨z=−3±4i but z=3+2(√2) doesn′t solve the given equation ⇒ z=3−2(√2)∧z+2(√z)=1 ∨ z=−3±4i∧z+2(√z)=−1±8i
$$\mathrm{if}\:\mathrm{you}\:\mathrm{know}\:\mathrm{nothing}\:\mathrm{you}\:\mathrm{must}\:\mathrm{believe} \\ $$$$\mathrm{everything} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{methodically}\:\mathrm{wrong} \\ $$$$\mathrm{you}\:\mathrm{show}\:\mathrm{me}\:\mathrm{how}\:{z}+\mathrm{2}\sqrt{{z}}=−\mathrm{5}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved} \\ $$$$ \\ $$$${z}>\mathrm{0}\wedge\sqrt{{z}}={u}\:\Rightarrow\:{u}>\mathrm{0} \\ $$$${u}^{\mathrm{4}} +\mathrm{12}{u}−\mathrm{5}=\mathrm{0} \\ $$$$\left({u}^{\mathrm{2}} −{au}−{b}\right)\left({u}^{\mathrm{2}} +{au}−{c}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{a}^{\mathrm{2}} +{b}+{c}=\mathrm{0}}\\{{a}\left({c}−{b}\right)−\mathrm{12}=\mathrm{0}}\\{{bc}+\mathrm{5}=\mathrm{0}}\end{cases}\:\Leftrightarrow\:{a}=\mathrm{2}\wedge{b}=−\mathrm{5}\wedge{c}=\mathrm{1} \\ $$$$\left({u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{5}\right)\left({u}^{\mathrm{2}} +\mathrm{2}{u}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${u}=−\mathrm{1}\pm\sqrt{\mathrm{2}}\vee{u}=\mathrm{1}\pm\mathrm{2i} \\ $$$${u}>\mathrm{0}\:\Rightarrow\:{u}=−\mathrm{1}+\sqrt{\mathrm{2}}=\sqrt{{z}}\:\Rightarrow\:{z}=\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${z}+\mathrm{2}\sqrt{{z}}=\mathrm{1} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{drop}\:{z}>\mathrm{0} \\ $$$${z}={u}^{\mathrm{2}} \\ $$$${z}=\mathrm{3}\pm\mathrm{2}\sqrt{\mathrm{2}}\vee{z}=−\mathrm{3}\pm\mathrm{4i} \\ $$$$\mathrm{but}\:{z}=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$$$\Rightarrow \\ $$$${z}=\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\wedge{z}+\mathrm{2}\sqrt{{z}}=\mathrm{1} \\ $$$$\vee \\ $$$${z}=−\mathrm{3}\pm\mathrm{4i}\wedge{z}+\mathrm{2}\sqrt{{z}}=−\mathrm{1}\pm\mathrm{8i} \\ $$
Commented by mathdanisur last updated on 06/Aug/21
Thank you Ser, cool
$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{Ser}},\:\mathrm{cool} \\ $$
Answered by MJS_new last updated on 04/Aug/21
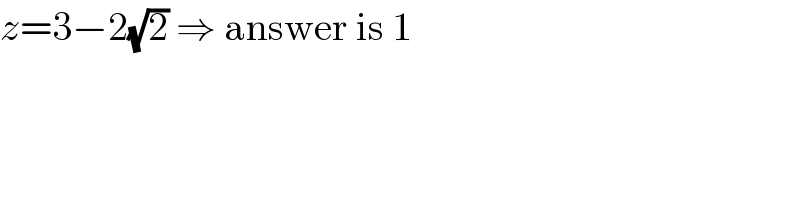
z=3−2(√2) ⇒ answer is 1
$${z}=\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *