Question Number 118984 by 675480065 last updated on 21/Oct/20
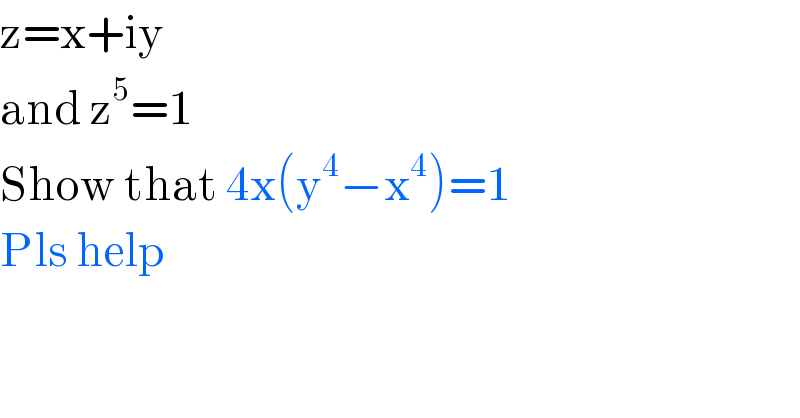
$$\mathrm{z}=\mathrm{x}+\mathrm{iy} \\ $$$$\mathrm{and}\:\mathrm{z}^{\mathrm{5}} =\mathrm{1} \\ $$$$\mathrm{Show}\:\mathrm{that}\:\mathrm{4x}\left(\mathrm{y}^{\mathrm{4}} −\mathrm{x}^{\mathrm{4}} \right)=\mathrm{1} \\ $$$$\mathrm{Pls}\:\mathrm{help} \\ $$
Answered by Dwaipayan Shikari last updated on 21/Oct/20
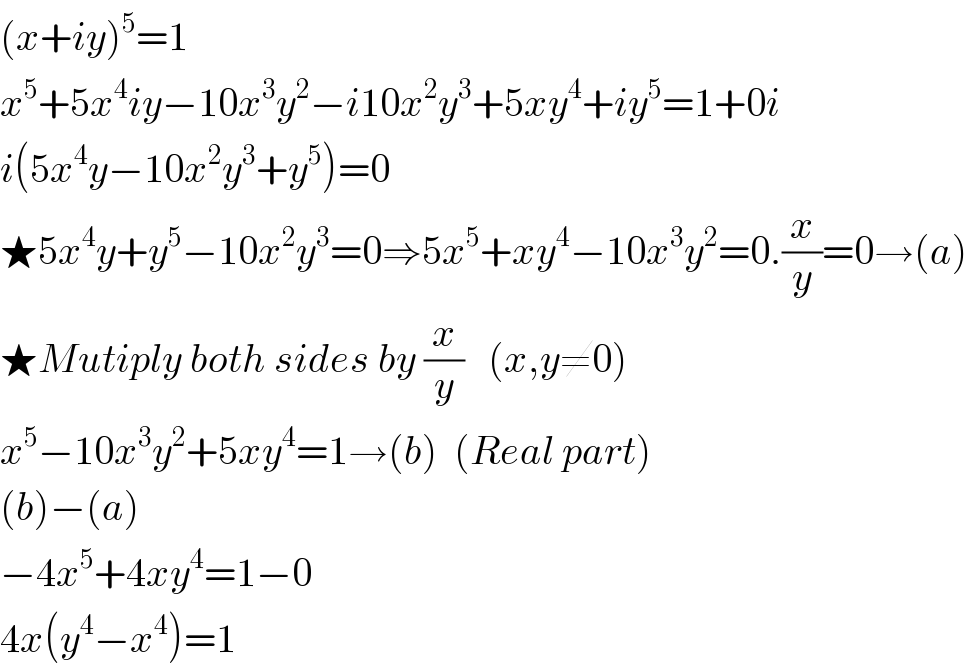
$$\left({x}+{iy}\right)^{\mathrm{5}} =\mathrm{1} \\ $$$${x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} {iy}−\mathrm{10}{x}^{\mathrm{3}} {y}^{\mathrm{2}} −{i}\mathrm{10}{x}^{\mathrm{2}} {y}^{\mathrm{3}} +\mathrm{5}{xy}^{\mathrm{4}} +{iy}^{\mathrm{5}} =\mathrm{1}+\mathrm{0}{i} \\ $$$${i}\left(\mathrm{5}{x}^{\mathrm{4}} {y}−\mathrm{10}{x}^{\mathrm{2}} {y}^{\mathrm{3}} +{y}^{\mathrm{5}} \right)=\mathrm{0} \\ $$$$\bigstar\mathrm{5}{x}^{\mathrm{4}} {y}+{y}^{\mathrm{5}} −\mathrm{10}{x}^{\mathrm{2}} {y}^{\mathrm{3}} =\mathrm{0}\Rightarrow\mathrm{5}{x}^{\mathrm{5}} +{xy}^{\mathrm{4}} −\mathrm{10}{x}^{\mathrm{3}} {y}^{\mathrm{2}} =\mathrm{0}.\frac{{x}}{{y}}=\mathrm{0}\rightarrow\left({a}\right) \\ $$$$\bigstar{Mutiply}\:{both}\:{sides}\:{by}\:\frac{{x}}{{y}}\:\:\:\left({x},{y}\neq\mathrm{0}\right) \\ $$$${x}^{\mathrm{5}} −\mathrm{10}{x}^{\mathrm{3}} {y}^{\mathrm{2}} +\mathrm{5}{xy}^{\mathrm{4}} =\mathrm{1}\rightarrow\left({b}\right)\:\:\left({Real}\:{part}\right) \\ $$$$\left({b}\right)−\left({a}\right) \\ $$$$−\mathrm{4}{x}^{\mathrm{5}} +\mathrm{4}{xy}^{\mathrm{4}} =\mathrm{1}−\mathrm{0} \\ $$$$\mathrm{4}{x}\left({y}^{\mathrm{4}} −{x}^{\mathrm{4}} \right)=\mathrm{1} \\ $$
Commented by 675480065 last updated on 21/Oct/20

$$\boldsymbol{\mathrm{T}}\mathrm{Hankz} \\ $$
