Question Number 193149 by Mingma last updated on 04/Jun/23
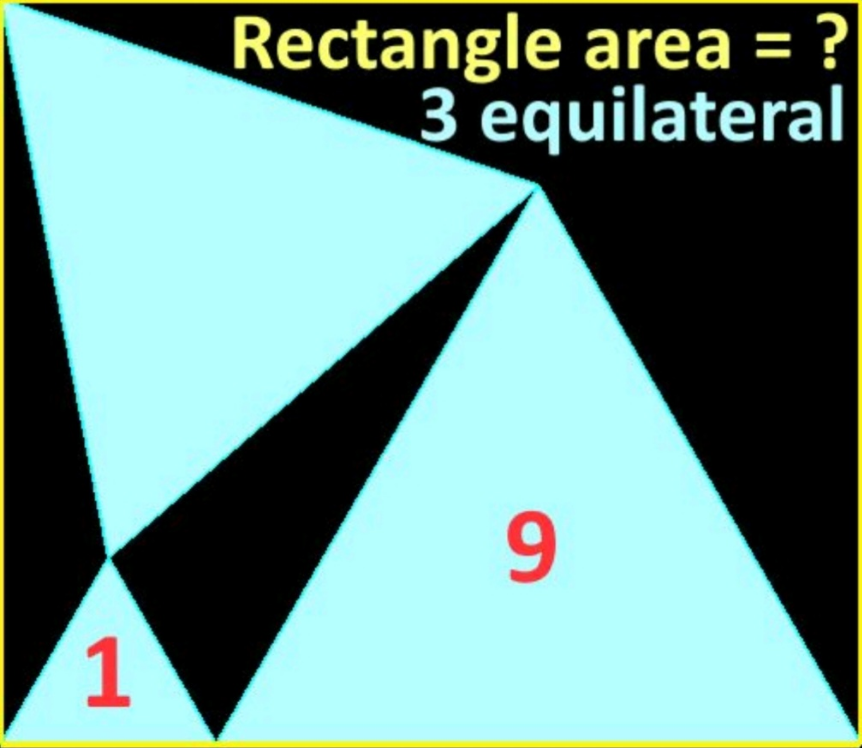
Answered by ajfour last updated on 05/Jun/23

$$\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{p}^{\mathrm{2}} ={A} \\ $$$${p}={k}\sqrt{{A}}\:\:\:\:{where}\:\:\:{k}^{\mathrm{2}} =\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}} \\ $$$${q}={k}\sqrt{{B}} \\ $$$${B}=\mathrm{9}{A} \\ $$$${P}\left(\frac{{p}}{\mathrm{2}},\frac{{p}\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${Q}\left(\frac{\mathrm{2}{p}+{q}}{\mathrm{2}},\:\frac{{q}\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${q}=\mathrm{3}{p}\:\:\:\: \\ $$$${PQ}=\sqrt{\left(\frac{{p}+{q}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{3}\left(\frac{{q}−{p}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${PQ}={c}=\sqrt{\mathrm{7}}{p} \\ $$$${m}=\frac{\left({q}−{p}\right)\sqrt{\mathrm{3}}}{{q}+{p}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${M}\left(\frac{\mathrm{3}{p}+{q}}{\mathrm{4}},\frac{\left({p}+{q}\right)\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$${M}\left(\frac{\mathrm{3}{p}}{\mathrm{2}},\:\sqrt{\mathrm{3}}{p}\right) \\ $$$$\frac{{c}\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{21}}}{\mathrm{2}}{p} \\ $$$$\mathrm{tan}\:\phi=\frac{\mathrm{1}}{{m}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\:\Rightarrow\:\:\mathrm{sin}\:\phi=\frac{\mathrm{2}}{\:\sqrt{\mathrm{7}}} \\ $$$${H}={y}_{{M}} +\frac{{c}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{sin}\:\phi \\ $$$$\:\:\:\:=\sqrt{\mathrm{3}}{p}+\frac{{p}\sqrt{\mathrm{7}}\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{7}}} \\ $$$$\:\:\:=\mathrm{2}\sqrt{\mathrm{3}}{p} \\ $$$${p}={k}\:\:{as}\:\:{A}=\mathrm{1} \\ $$$${H}=\mathrm{2}\sqrt{\mathrm{3}}{k} \\ $$$${W}={p}+{q}=\mathrm{4}{p}=\mathrm{4}{k} \\ $$$${Rectangle}\:{area}={WH} \\ $$$$\:\:\:=\left(\mathrm{4}{k}\right)\left(\mathrm{2}\sqrt{\mathrm{3}}{k}\right)=\mathrm{8}\sqrt{\mathrm{3}}{k}^{\mathrm{2}} \\ $$$$\:\:\:=\mathrm{8}\sqrt{\mathrm{3}}×\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}=\:\mathrm{32}\:\:{sq}.\:{units}. \\ $$
Commented by Mingma last updated on 05/Jun/23
Perfect ��
I'm excited you corrected yourself!
