Menu Close

Question-193161

Tinku Tara 0 Comments
Pin




Question Number 193161 by Mingma last updated on 05/Jun/23
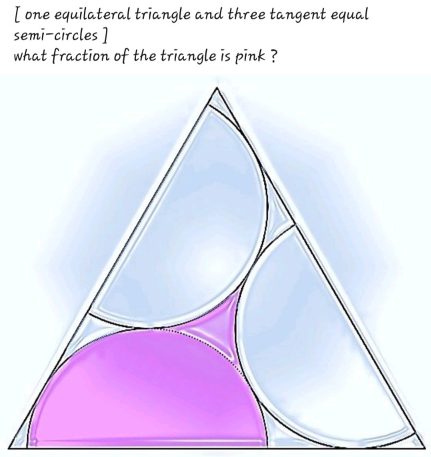
Answered by a.lgnaoui last updated on 05/Jun/23
Triangle ABC equilaterale MN=NP=MP ∡BAH=60=∡DAH ⇒ ∡ADH=30° ∡AMN=90−30=60 MNP Triangle equilaterale MN=NP=MP Area(MNP)=Aeea(arc( MN)− area(triangleDMN) Aera(triangkeD MN)=R×Rsin (π/3)=((R^2 (√3))/2) Area(arc MN)=((πR^2 )/3) arc=((πR^2 )/3)−((R^2 (√3))/2)=(((2π−3(√3))R^2 )/6) Aeea(MNP)=Area(triangle MNP) −2Area(arcMN) Area=((R^2 (√3))/2)−2(((2π−3(√3))R^2 )/6)=((3R^2 −(4π−6(√3))R^2 )/6) Area(pink triangle)=(((6(√3) +3−4𝛑)R^2 )/6) =((√3) +((3−4π)/6))R^2 =0,1377R^2 aire (pink area)=(π/2)R^2 +((√3) +((3−4π)/6))R^2 =((√3) +((3−π)/6))R^2 ((√3) +(1/2)+(π/6))R^2 =0,795R^2 ⇒fraction=((0,1377)/(0,795))=17%
$$\mathrm{Triangle}\:\mathrm{ABC}\:\:\mathrm{equilaterale}\: \\ $$$$\boldsymbol{\mathrm{MN}}=\boldsymbol{\mathrm{NP}}=\boldsymbol{\mathrm{MP}} \\ $$$$\measuredangle\mathrm{BAH}=\mathrm{60}=\measuredangle\mathrm{DAH} \\ $$$$\Rightarrow\:\measuredangle\mathrm{ADH}=\mathrm{30}°\:\:\:\measuredangle\mathrm{AMN}=\mathrm{90}−\mathrm{30}=\mathrm{60} \\ $$$$\mathrm{MNP}\:\:\:\mathrm{Triangle}\:\mathrm{equilaterale} \\ $$$$\mathrm{MN}=\mathrm{NP}=\mathrm{MP} \\ $$$$\:\mathrm{Area}\left(\mathrm{MNP}\right)=\mathrm{Aeea}\left(\mathrm{arc}\left(\:\mathrm{MN}\right)−\right. \\ $$$$\mathrm{area}\left(\mathrm{triangleDMN}\right) \\ $$$$\mathrm{Aera}\left(\mathrm{triangkeD}\:\mathrm{MN}\right)=\mathrm{R}×\mathrm{Rsin}\:\frac{\pi}{\mathrm{3}}=\frac{\mathrm{R}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{Area}\left(\mathrm{arc}\:\mathrm{MN}\right)=\frac{\pi\mathrm{R}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\mathrm{arc}=\frac{\pi\mathrm{R}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{R}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\left(\mathrm{2}\pi−\mathrm{3}\sqrt{\mathrm{3}}\right)\mathrm{R}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\mathrm{Aeea}\left(\mathrm{MNP}\right)=\mathrm{Area}\left(\mathrm{triangle}\:\mathrm{MNP}\right) \\ $$$$−\mathrm{2Area}\left(\mathrm{arcMN}\right) \\ $$$$ \\ $$$$\mathrm{Area}=\frac{\mathrm{R}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{2}\frac{\left(\mathrm{2}\pi−\mathrm{3}\sqrt{\mathrm{3}}\right)\mathrm{R}^{\mathrm{2}} }{\mathrm{6}}=\frac{\mathrm{3R}^{\mathrm{2}} −\left(\mathrm{4}\pi−\mathrm{6}\sqrt{\mathrm{3}}\right)\mathrm{R}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\mathrm{Area}\left(\mathrm{pink}\:\mathrm{triangle}\right)=\frac{\left(\mathrm{6}\sqrt{\mathrm{3}}\:+\mathrm{3}−\mathrm{4}\boldsymbol{\pi}\right)\boldsymbol{\mathrm{R}}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=\left(\sqrt{\mathrm{3}}\:+\frac{\mathrm{3}−\mathrm{4}\pi}{\mathrm{6}}\right)\mathrm{R}^{\mathrm{2}} \\ $$$$=\mathrm{0},\mathrm{1377R}^{\mathrm{2}} \\ $$$$\mathrm{aire}\:\left(\mathrm{pink}\:\mathrm{area}\right)=\frac{\pi}{\mathrm{2}}\mathrm{R}^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\:+\frac{\mathrm{3}−\mathrm{4}\pi}{\mathrm{6}}\right)\mathrm{R}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\sqrt{\mathrm{3}}\:+\frac{\mathrm{3}−\pi}{\mathrm{6}}\right)\mathrm{R}^{\mathrm{2}} \\ $$$$\left(\sqrt{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{6}}\right)\mathrm{R}^{\mathrm{2}} =\mathrm{0},\mathrm{795R}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{fraction}=\frac{\mathrm{0},\mathrm{1377}}{\mathrm{0},\mathrm{795}}=\mathrm{17\%} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 07/Jun/23

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *