Question Number 53384 by gunawan last updated on 21/Jan/19
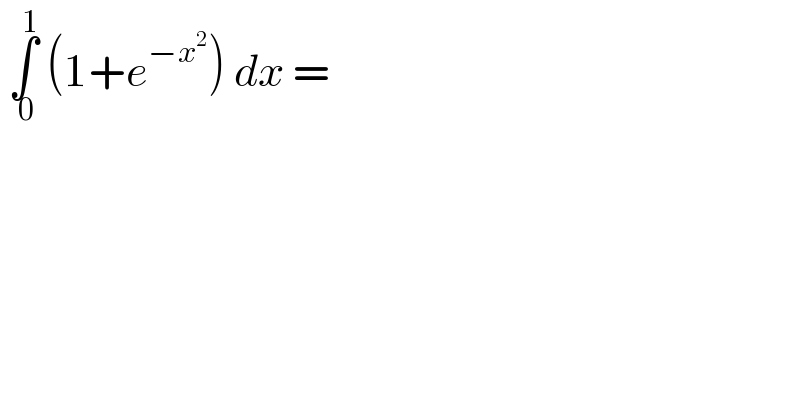
$$\:\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left(\mathrm{1}+{e}^{−{x}^{\mathrm{2}} } \right)\:{dx}\:= \\ $$
Commented by Abdo msup. last updated on 21/Jan/19

$${we}\:{have}\:{e}^{{u}} =\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}} }{{n}!}\:\Rightarrow{e}^{−{x}^{\mathrm{2}} } =\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{{n}!}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{e}^{−{x}^{\mathrm{2}} } {dx}\:=\mathrm{1}+\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{x}^{\mathrm{2}} } {dx}\right. \\ $$$$=\mathrm{1}+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{n}} {dx} \\ $$$$=\mathrm{1}+\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!} \\ $$$$=\mathrm{1}+\mathrm{1}\:−\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{5}\left(\mathrm{2}!\right)}\:−\frac{\mathrm{1}}{\mathrm{7}\left(\mathrm{3}!\right)}\:+\frac{\mathrm{1}}{\mathrm{9}\left(\mathrm{4}!\right)}\:−\frac{\mathrm{1}}{\mathrm{11}\left(\mathrm{5}!\right)}\:+… \\ $$$$=\frac{\mathrm{5}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{10}}\:−\frac{\mathrm{1}}{\mathrm{42}}\:+…. \\ $$$${we}\:{get}\:{best}\:{approximation}\:{for}\:{this}\:{integral} \\ $$$${if}\:{we}\:{take}\:\mathrm{10}\:{terms}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19

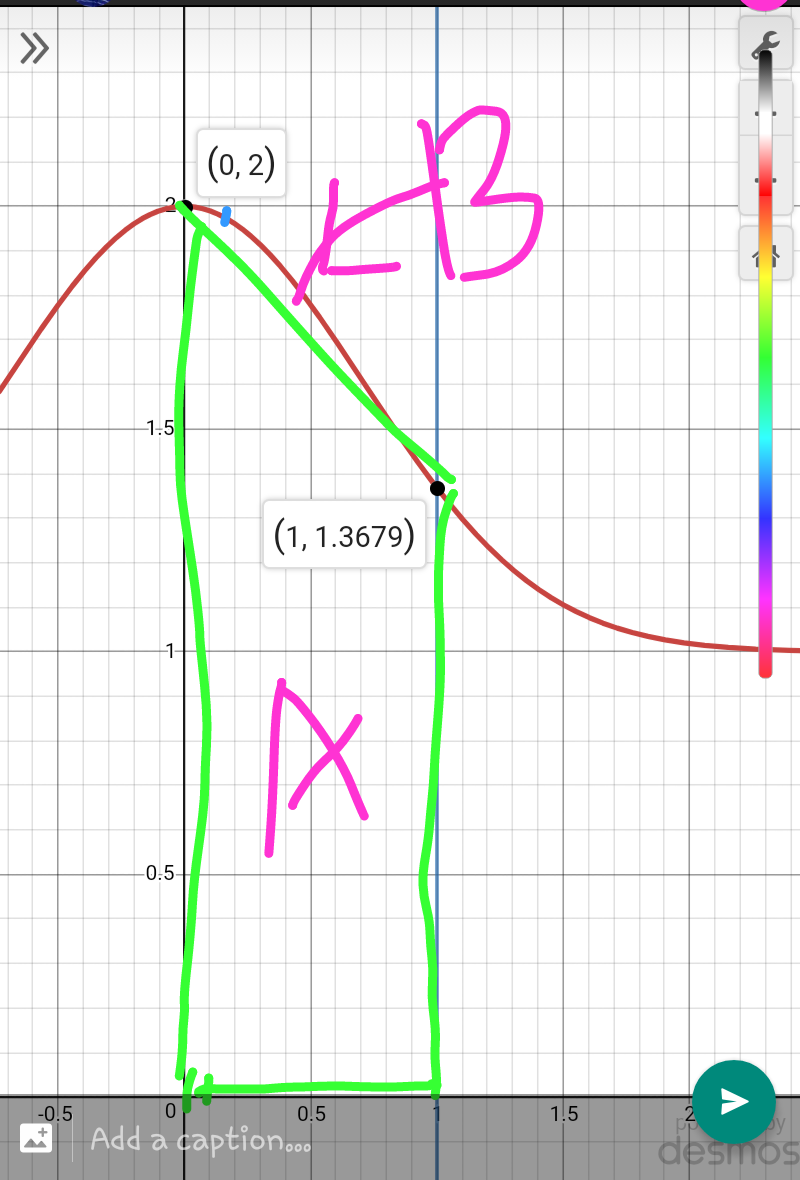
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{\mathrm{1}}{{e}^{{x}^{\mathrm{2}} } }\right){dx} \\ $$$${this}\:{intrgal}\:{can}\:{be}\:{solved}\:{withthe}\:{help}\:{of}\:{graph} \\ $$$${f}\left({x}\right)=\mathrm{1}+\frac{\mathrm{1}}{{e}^{{x}^{\mathrm{2}} } } \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{2} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}+{e}^{−\mathrm{1}} \\ $$$$=\mathrm{0}<\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{\mathrm{1}}{{e}^{{x}^{\mathrm{2}} } }\right)<\frac{\mathrm{1}}{\mathrm{2}}\left\{{f}\left(\mathrm{0}\right)+{f}\left(\mathrm{1}\right)\right\}×\mathrm{1} \\ $$$$\:\:\mathrm{0}<{I}<\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}+\mathrm{1}+{e}^{−\mathrm{1}} \right) \\ $$$$\mathrm{0}<{I}<\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}+\frac{\mathrm{1}}{{e}}\right) \\ $$$$\mathrm{0}<{I}<\mathrm{1}.\mathrm{68} \\ $$$${but}\:{from}\:{attached}\:{graph}\:{the}\:{area}\:{is}\:{A}+{B} \\ $$$${but}\:{we}\:{found}\:{A}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}+\frac{\mathrm{1}}{{e}}\right) \\ $$$${so}\:{actual}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{\mathrm{1}}{{e}^{{x}^{\mathrm{2}} } }\right){dx}={A}+{B} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19