Question Number 21398 by math1967 last updated on 23/Sep/17
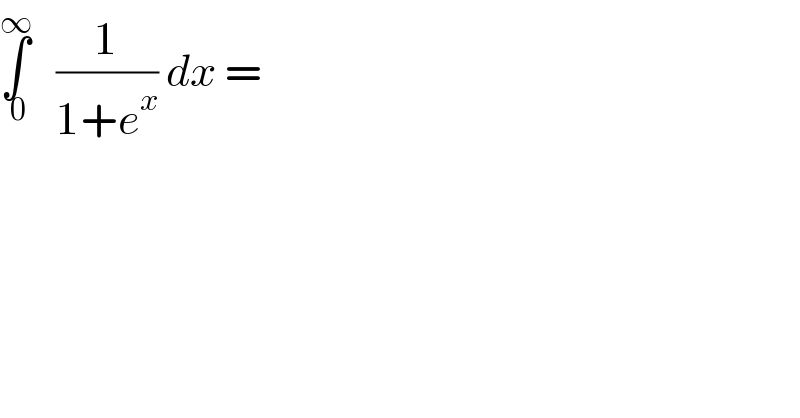
$$\underset{\:\mathrm{0}} {\overset{\infty} {\int}}\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{e}^{{x}} }\:{dx}\:= \\ $$
Answered by sma3l2996 last updated on 23/Sep/17
![e^x =t⇒dx=(dt/t) ∫_0 ^∞ (dx/(1+e^x ))=∫_1 ^∞ (dt/(t(t+1)))=∫_1 ^∞ (dt/t)−∫_1 ^∞ (dx/(1+t))=[ln((t/(1+t)))]_1 ^∞ ∫_0 ^∞ (dx/(1+e^x ))=lim_(x→∞) ln((t/(1+t)))−ln((1/2))=ln((1/((1/t)+1)))+ln2 ∫_0 ^∞ (dx/(1+e^x ))=ln(1)+ln2=ln(2)](https://www.tinkutara.com/question/Q21399.png)
$${e}^{{x}} ={t}\Rightarrow{dx}=\frac{{dt}}{{t}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{e}^{{x}} }=\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{{t}\left({t}+\mathrm{1}\right)}=\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{{t}}−\int_{\mathrm{1}} ^{\infty} \frac{{dx}}{\mathrm{1}+{t}}=\left[{ln}\left(\frac{{t}}{\mathrm{1}+{t}}\right)\right]_{\mathrm{1}} ^{\infty} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{e}^{{x}} }=\underset{{x}\rightarrow\infty} {{lim}ln}\left(\frac{{t}}{\mathrm{1}+{t}}\right)−{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)={ln}\left(\frac{\mathrm{1}}{\frac{\mathrm{1}}{{t}}+\mathrm{1}}\right)+{ln}\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{e}^{{x}} }={ln}\left(\mathrm{1}\right)+{ln}\mathrm{2}={ln}\left(\mathrm{2}\right) \\ $$
