Menu Close

0-1-1-x-1-x-3-dx-15-8-

Tinku Tara 0 Comments
Pin




Question Number 57140 by mustakim420 last updated on 30/Mar/19
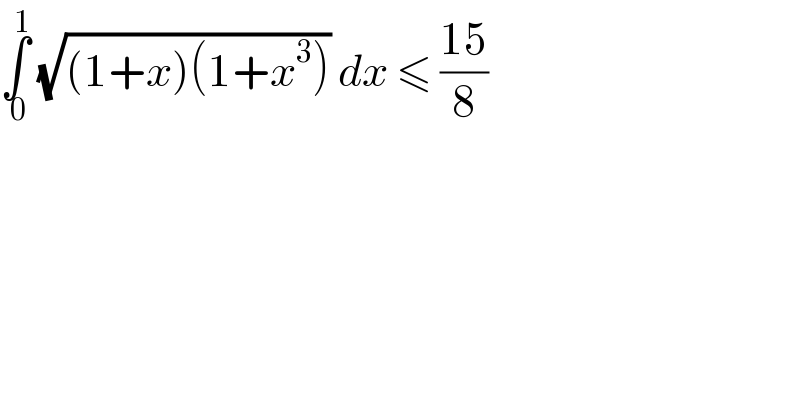
∫_( 0) ^1 (√((1+x)(1+x^3 ))) dx ≤ ((15)/8)
$$\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\sqrt{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)}\:{dx}\:\leqslant\:\frac{\mathrm{15}}{\mathrm{8}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 30/Mar/19
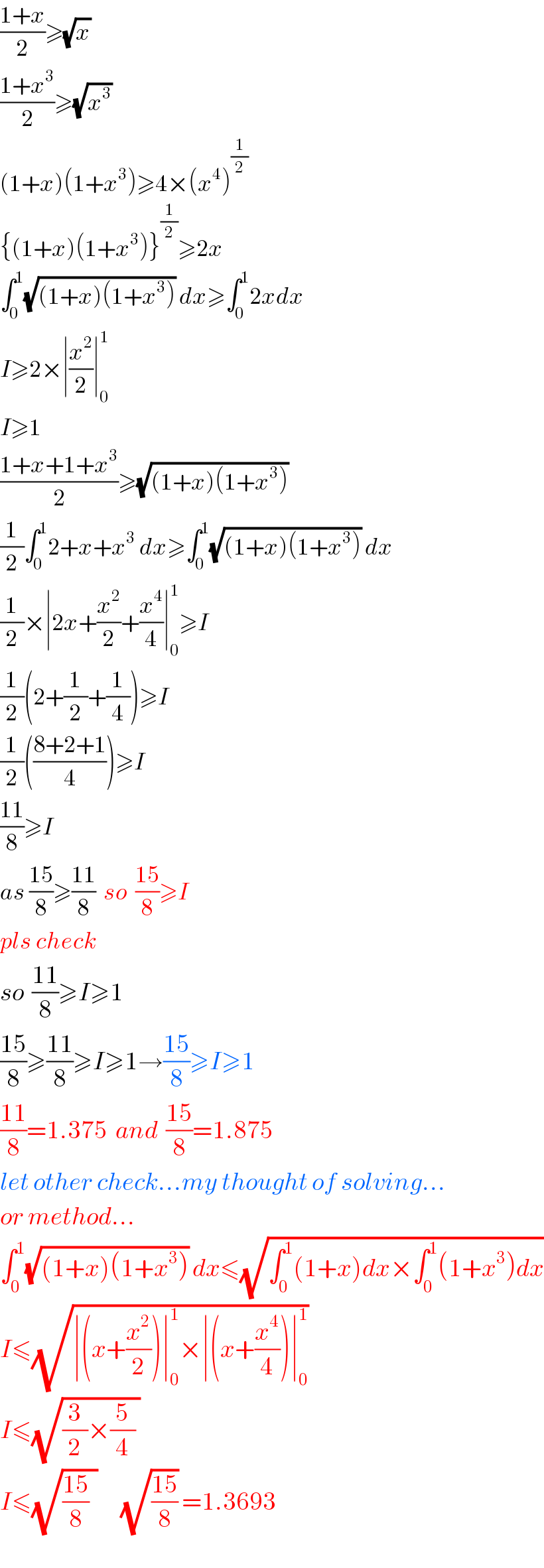
((1+x)/2)≥(√x) ((1+x^3 )/2)≥(√x^3 ) (1+x)(1+x^3 )≥4×(x^4 )^(1/2) {(1+x)(1+x^3 )}^(1/2) ≥2x ∫_0 ^1 (√((1+x)(1+x^3 ))) dx≥∫_0 ^1 2xdx I≥2×∣(x^2 /2)∣_0 ^1 I≥1 ((1+x+1+x^3 )/2)≥(√((1+x)(1+x^3 ))) (1/2)∫_0 ^1 2+x+x^3 dx≥∫_0 ^1 (√((1+x)(1+x^3 ))) dx (1/2)×∣2x+(x^2 /2)+(x^4 /4)∣_0 ^1 ≥I (1/2)(2+(1/2)+(1/4))≥I (1/2)(((8+2+1)/4))≥I ((11)/8)≥I as ((15)/8)≥((11)/8) so ((15)/8)≥I pls check so ((11)/8)≥I≥1 ((15)/8)≥((11)/8)≥I≥1→((15)/8)≥I≥1 ((11)/8)=1.375 and ((15)/8)=1.875 let other check...my thought of solving... or method... ∫_0 ^1 (√((1+x)(1+x^3 ))) dx≤(√(∫_0 ^1 (1+x)dx×∫_0 ^1 (1+x^3 )dx)) I≤(√(∣(x+(x^2 /2))∣_0 ^1 ×∣(x+(x^4 /4))∣_0 ^1 )) I≤(√((3/2)×(5/4) )) I≤(√(((15)/8) )) (√((15)/8)) =1.3693
$$\frac{\mathrm{1}+{x}}{\mathrm{2}}\geqslant\sqrt{{x}}\: \\ $$$$\frac{\mathrm{1}+{x}^{\mathrm{3}} }{\mathrm{2}}\geqslant\sqrt{{x}^{\mathrm{3}} }\: \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)\geqslant\mathrm{4}×\left({x}^{\mathrm{4}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\left\{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)\right\}^{\frac{\mathrm{1}}{\mathrm{2}}} \geqslant\mathrm{2}{x} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)}\:{dx}\geqslant\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}{xdx} \\ $$$${I}\geqslant\mathrm{2}×\mid\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${I}\geqslant\mathrm{1} \\ $$$$\frac{\mathrm{1}+{x}+\mathrm{1}+{x}^{\mathrm{3}} }{\mathrm{2}}\geqslant\sqrt{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}+{x}+{x}^{\mathrm{3}} \:{dx}\geqslant\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)}\:{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mid\mathrm{2}{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\mid_{\mathrm{0}} ^{\mathrm{1}} \geqslant{I} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\geqslant{I} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{8}+\mathrm{2}+\mathrm{1}}{\mathrm{4}}\right)\geqslant{I} \\ $$$$\frac{\mathrm{11}}{\mathrm{8}}\geqslant{I} \\ $$$${as}\:\frac{\mathrm{15}}{\mathrm{8}}\geqslant\frac{\mathrm{11}}{\mathrm{8}}\:\:{so}\:\:\frac{\mathrm{15}}{\mathrm{8}}\geqslant{I} \\ $$$${pls}\:{check}\: \\ $$$${so}\:\:\frac{\mathrm{11}}{\mathrm{8}}\geqslant{I}\geqslant\mathrm{1} \\ $$$$\frac{\mathrm{15}}{\mathrm{8}}\geqslant\frac{\mathrm{11}}{\mathrm{8}}\geqslant{I}\geqslant\mathrm{1}\rightarrow\frac{\mathrm{15}}{\mathrm{8}}\geqslant{I}\geqslant\mathrm{1} \\ $$$$\frac{\mathrm{11}}{\mathrm{8}}=\mathrm{1}.\mathrm{375}\:\:{and}\:\:\frac{\mathrm{15}}{\mathrm{8}}=\mathrm{1}.\mathrm{875} \\ $$$${let}\:{other}\:{check}…{my}\:{thought}\:{of}\:{solving}… \\ $$$${or}\:{method}… \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)}\:{dx}\leqslant\sqrt{\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}\right){dx}×\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx}} \\ $$$${I}\leqslant\sqrt{\mid\left({x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} ×\mid\left({x}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} }\: \\ $$$${I}\leqslant\sqrt{\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{5}}{\mathrm{4}}\:} \\ $$$${I}\leqslant\sqrt{\frac{\mathrm{15}}{\mathrm{8}}\:\:}\:\:\:\:\:\:\sqrt{\frac{\mathrm{15}}{\mathrm{8}}}\:=\mathrm{1}.\mathrm{3693} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *