Menu Close

0-1-1-x-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 115404 by EvoneAkashi last updated on 25/Sep/20
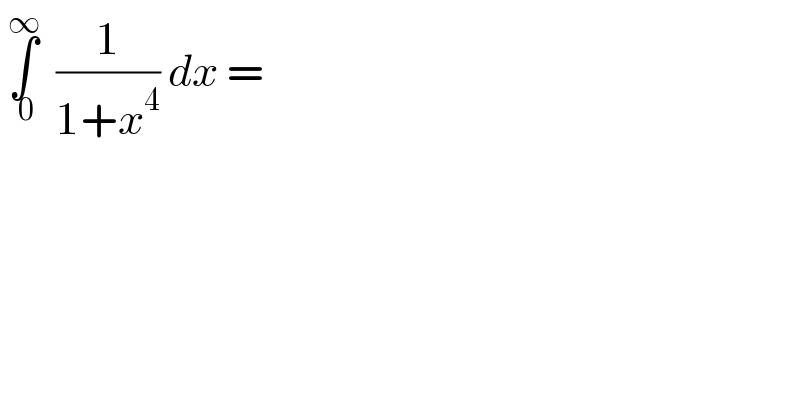
∫_( 0) ^∞ (1/(1+x^4 )) dx =
$$\:\underset{\:\mathrm{0}} {\overset{\infty} {\int}}\:\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx}\:= \\ $$
Answered by mathmax by abdo last updated on 25/Sep/20
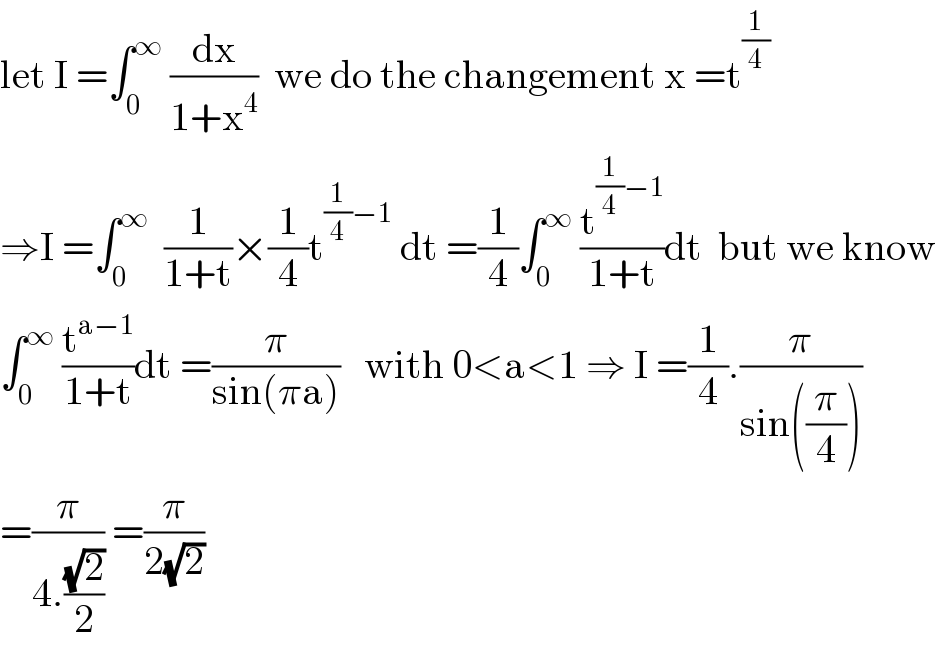
let I =∫_0 ^∞ (dx/(1+x^4 )) we do the changement x =t^(1/4) ⇒I =∫_0 ^∞ (1/(1+t))×(1/4)t^((1/4)−1) dt =(1/4)∫_0 ^∞ (t^((1/4)−1) /(1+t))dt but we know ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) with 0<a<1 ⇒ I =(1/4).(π/(sin((π/4)))) =(π/(4.((√2)/2))) =(π/(2(√2)))
$$\mathrm{let}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}}×\frac{\mathrm{1}}{\mathrm{4}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:\:\mathrm{but}\:\mathrm{we}\:\mathrm{know} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{a}\right)}\:\:\:\mathrm{with}\:\mathrm{0}<\mathrm{a}<\mathrm{1}\:\Rightarrow\:\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{4}}.\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)} \\ $$$$=\frac{\pi}{\mathrm{4}.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Answered by Dwaipayan Shikari last updated on 25/Sep/20
∫_0 ^∞ (1/(1+x^4 ))dx=∫_0 ^(π/2) (1/(2x)) ((2x)/(1+tan^2 θ ))sec^2 θdθ x^2 =tanθ⇒2x=sec^2 θ(dθ/dx) (1/2)∫_0 ^(π/2) (1/( (√(tanθ))))dθ=(1/2)∫_0 ^(π/2) (1/( (√(cotθ))))=I 2I=(1/2)∫_0 ^(π/2) ((sinθ+cosθ)/( (√(sinθcosθ))))dθ 4I=(√2)∫_0 ^(π/2) ((sinθ+cosθ)/( (√(1−(sinθ−cosθ)^2 ))))dθ 2(√2)I=∫_(−1) ^1 (dt/( (√(1−t^2 )))) (√2)I=∫_0 ^1 (dt/( (√(1−t^2 )))) (√2) I=[sin^(−1) (t)]_0 ^1 (√2) I=(π/2)⇒I=(π/(2(√2)))
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2x}}\:\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\:}\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} =\mathrm{tan}\theta\Rightarrow\mathrm{2x}=\mathrm{sec}^{\mathrm{2}} \theta\frac{\mathrm{d}\theta}{\mathrm{dx}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\theta}}\mathrm{d}\theta=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{cot}\theta}}=\mathrm{I} \\ $$$$\mathrm{2I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}\theta+\mathrm{cos}\theta}{\:\sqrt{\mathrm{sin}\theta\mathrm{cos}\theta}}\mathrm{d}\theta \\ $$$$\mathrm{4I}=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sin}\theta+\mathrm{cos}\theta}{\:\sqrt{\mathrm{1}−\left(\mathrm{sin}\theta−\mathrm{cos}\theta\right)^{\mathrm{2}} }}\mathrm{d}\theta \\ $$$$\mathrm{2}\sqrt{\mathrm{2}}\mathrm{I}=\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }} \\ $$$$\sqrt{\mathrm{2}}\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }} \\ $$$$\sqrt{\mathrm{2}}\:\mathrm{I}=\left[\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\sqrt{\mathrm{2}}\:\mathrm{I}=\frac{\pi}{\mathrm{2}}\Rightarrow\mathrm{I}=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$ \\ $$
Answered by TANMAY PANACEA last updated on 25/Sep/20
(1/2)∫((2×(1/x^2 ))/(x^2 +(1/x^2 )))dx (1/2)∫((d(x−(1/x))−d(x+(1/x)))/(x^2 +(1/x^2 ))) (1/2)∫((d(x−(1/x)))/((x−(1/x))^2 +2))−(1/2)∫((d(x+(1/x)))/((x+(1/x))^2 −2)) now use formula pls..Tanmay
$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}×\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)−{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$${now}\:{use}\:{formula}\:{pls}..{Tanmay} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 26/Sep/20
complex method 2I =∫_(−∞) ^(+∞) (dx/(x^4 +1)) =∫_(−∞) ^(+∞) (dx/((x^2 −i)(x^2 +i))) =(1/(2i))∫_(−∞) ^(+∞) ((1/(x^2 −i))−(1/(x^2 +i))) =(1/(2i)) (∫_(−∞) ^(+∞ ) (dx/(x^2 −i)) −∫_(−∞) ^(+∞ ) (dx/(x^2 +i))) =(1/(2i))(2i Im(∫_(−∞) ^(+∞) (dx/(x^2 −i)))) =Im(∫_(−∞) ^(+∞) (dx/(x^2 −i))) let ϕ(z) =(1/(z^2 −i)) we have ϕ(z) =(1/((z−e^((iπ)/4) )(z+e^((iπ)/4) ))) residus theorem give ∫_(−∞) ^(+∞) ϕ−z)dz =2iπ Res(ϕ,e^((iπ)/4) ) =2iπ.(1/(2e^((iπ)/4) )) =iπ e^(−((iπ)/4)) =iπ{(1/( (√2)))−(i/( (√2)))} =((iπ)/( (√2))) +(π/( (√2))) ⇒2I =(π/( (√2))) ⇒ I =(π/(2(√2)))
$$\mathrm{complex}\:\mathrm{method}\:\:\:\:\mathrm{2I}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}\:=\int_{−\infty} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{i}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{i}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2i}}\int_{−\infty} ^{+\infty} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{i}}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{i}}\right)\:=\frac{\mathrm{1}}{\mathrm{2i}}\:\left(\int_{−\infty} ^{+\infty\:} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{i}}\:−\int_{−\infty} ^{+\infty\:} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{i}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2i}}\left(\mathrm{2i}\:\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{i}}\right)\right)\:=\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{i}}\right)\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} −\mathrm{i}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)}\:\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give} \\ $$$$\left.\int_{−\infty} ^{+\infty} \:\varphi−\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\:=\mathrm{2i}\pi.\frac{\mathrm{1}}{\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }\:=\mathrm{i}\pi\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \\ $$$$=\mathrm{i}\pi\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right\}\:=\frac{\mathrm{i}\pi}{\:\sqrt{\mathrm{2}}}\:+\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\mathrm{2I}\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\:\mathrm{I}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *