Question Number 85280 by Jakir Sarif Mondal last updated on 20/Mar/20
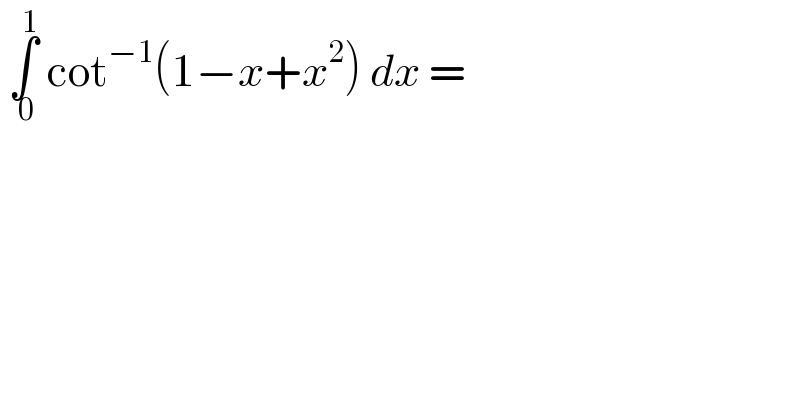
$$\:\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{cot}^{−\mathrm{1}} \left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)\:{dx}\:= \\ $$
Answered by mind is power last updated on 20/Mar/20
![=∫_0 ^1 tan^− ((1/(1−x(1−x))))dx =∫_0 ^1 tan^− (((1−x+x)/(1−x(1−x))))dx=∫_0 ^1 (tan^− (1−x)+tan^− (x))dx =2∫_0 ^1 tan^− (x)dx =2[xtan^− (x)−ln(1+x^2 )]_0 ^1_ =(π/2)−ln(2)](https://www.tinkutara.com/question/Q85283.png)
$$=\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−} \left(\frac{\mathrm{1}}{\mathrm{1}−{x}\left(\mathrm{1}−{x}\right)}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−} \left(\frac{\mathrm{1}−{x}+{x}}{\mathrm{1}−{x}\left(\mathrm{1}−{x}\right)}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left({tan}^{−} \left(\mathrm{1}−{x}\right)+{tan}^{−} \left({x}\right)\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−} \left({x}\right){dx} \\ $$$$=\mathrm{2}\left[{xtan}^{−} \left({x}\right)−{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}_{} } \\ $$$$=\frac{\pi}{\mathrm{2}}−{ln}\left(\mathrm{2}\right) \\ $$
