Question Number 81663 by zainal tanjung last updated on 14/Feb/20
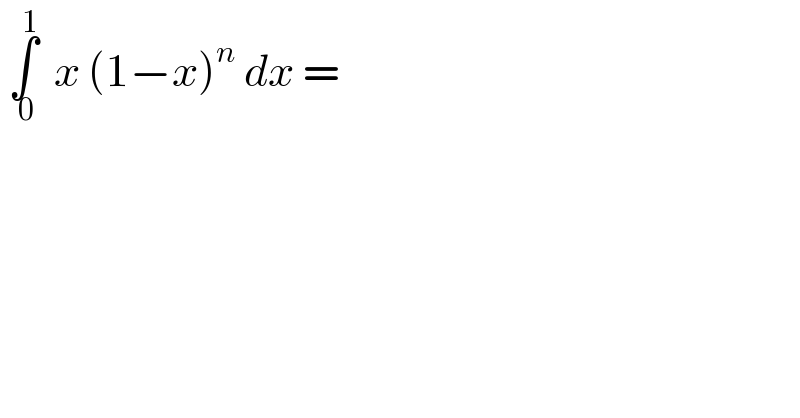
$$\:\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:{x}\:\left(\mathrm{1}−{x}\right)^{{n}} \:{dx}\:= \\ $$
Commented by Tony Lin last updated on 14/Feb/20

$${B}\left({p},\:{q}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{p}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{q}−\mathrm{1}} {dx},\:{p}>\mathrm{0},{q}>\mathrm{0} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\mathrm{1}−{x}\right)^{{n}} {dx} \\ $$$$={B}\left(\mathrm{2},\:{n}+\mathrm{1}\right) \\ $$$$=\frac{\Gamma\left(\mathrm{2}\right)\Gamma\left({n}+\mathrm{1}\right)}{\Gamma\left({n}+\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}×{n}!}{\left({n}+\mathrm{2}\right)!} \\ $$$$=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$
Commented by abdomathmax last updated on 14/Feb/20
![by parts u=x and v^(′ ) =(1−x)^n ∫_0 ^1 x(1−x)^n dx =[−(1/(n+1))x(1−x)^(n+1) ]_0 ^1 +∫_0 ^1 (1/(n+1))(1−x)^(n+1) dx =(1/(n+1))∫_0 ^1 (1−x)^(n+1) dx =(1/(n+1))×((−1)/(n+2))[(1−x)^(n+2) ]_0 ^1 =(1/((n+1)(n+2)))](https://www.tinkutara.com/question/Q81673.png)
$${by}\:{parts}\:{u}={x}\:{and}\:{v}^{'\:} =\left(\mathrm{1}−{x}\right)^{{n}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\mathrm{1}−{x}\right)^{{n}} \:{dx}\:=\left[−\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}\left(\mathrm{1}−{x}\right)^{{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\mathrm{1}−{x}\right)^{{n}+\mathrm{1}} \:{dx}\:=\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{n}+\mathrm{1}} \:{dx} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}×\frac{−\mathrm{1}}{{n}+\mathrm{2}}\left[\left(\mathrm{1}−{x}\right)^{{n}+\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$ \\ $$
