Question Number 58211 by salaw2000 last updated on 20/Apr/19
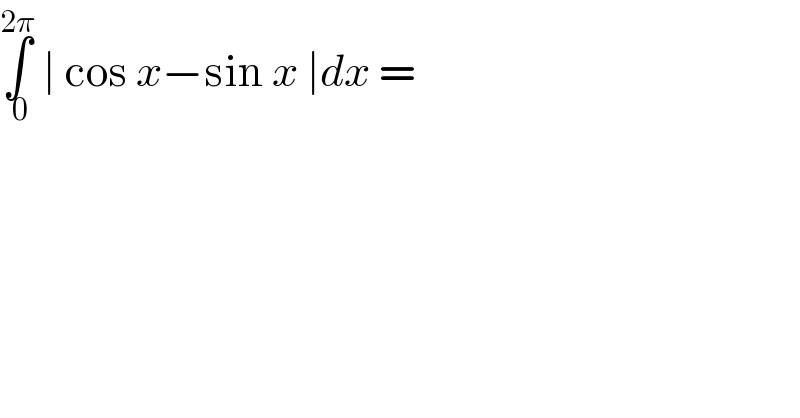
$$\underset{\:\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:\mid\:\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\:\mid{dx}\:= \\ $$
Commented by tanmay last updated on 20/Apr/19

Commented by tanmay last updated on 20/Apr/19

$${trying}\:{to}\:{solve}.. \\ $$$${see}\:{when}\:\:\frac{\pi}{\mathrm{4}}>{x}\geqslant\mathrm{0}\:\:{cosx}>{sinx}\:\:{so}\:\left({cosx}−{sinx}\right)>\mathrm{0}\:\mid{cosx}−{sinx}\mid=\left({cosx}−{sinx}\right) \\ $$$${when}\:\frac{\pi}{\mathrm{2}}>{x}\geqslant\frac{\pi}{\mathrm{4}}\:{cosx}<{sinx}\:{so}\left({cosx}−{sinx}\right)<\mathrm{0}\:\mid{cosx}−{sinx}\mid=−\left({cosx}−{sinx}\right) \\ $$$${when}\:\pi>{x}\geqslant\frac{\pi}{\mathrm{2}}\:{cosx}\:<\mathrm{0},\:{sinx}>\mathrm{0}\:{so}\left({cosx}−{sinx}\right)<\mathrm{0}\:\mid{cosx}−{sinx}\mid=−\left({cosx}−{sinx}\right) \\ $$$$\frac{\mathrm{5}\pi}{\mathrm{4}}>{x}\geqslant\pi\:\:\mid{cosx}\mid>\mid{sinx}\mid\:{so}\:\left({cosx}−{sinx}\right)<\mathrm{0}\:\mid{cosx}−{sinx}\mid=−\left({cosx}−{sinx}\right) \\ $$$$\frac{\mathrm{6}\pi}{\mathrm{4}}>{x}\geqslant\frac{\mathrm{5}\pi}{\mathrm{4}}\:\:\mid{cosx}\mid<\mid{sinx}\mid\:{so}\:\left({cosx}−{sinx}\right)>\mathrm{0}\:\:{so}\:\mid{cosx}−{sinx}\mid=\left({cosx}−{sinx}\right) \\ $$$$\mathrm{2}\pi>{x}\geqslant\frac{\mathrm{6}\pi}{\mathrm{4}}\:\:{cosx}>\mathrm{0}\:{but}\:{sinx}<\mathrm{0}\:\left({cosx}−{sinx}\right)>\mathrm{0}\:\mid{cosx}−{sinx}\mid=\left({cosx}−{sinx}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left({cosx}−{sinx}\right){dx}+\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} −\:\left({cosx}−{sinx}\right){dx}+ \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:−\left({cosx}−{sinx}\right){dx}+\int_{\pi} ^{\frac{\mathrm{5}\pi}{\mathrm{4}}} \:−\left({cosx}−{sinx}\right){dx} \\ $$$$\int_{\frac{\mathrm{5}\pi}{\mathrm{4}}} ^{\frac{\mathrm{6}\pi}{\mathrm{4}}} \:\left({cosx}−{sinx}\right){dx}+\int_{\frac{\mathrm{6}\pi}{\mathrm{4}}} ^{\mathrm{2}\pi} \:\left({cosx}−{sinx}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mid{cosx}−{sinx}\mid{dx}= \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left({cosx}−{sinx}\right){dx}+\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{5}\pi}{\mathrm{4}}} \:−\left({cosx}−{sinx}\right){dx}+\int_{\frac{\mathrm{5}\pi}{\mathrm{4}}} ^{\mathrm{2}\pi} \:\left({cosx}−{sinx}\right){dx} \\ $$$$\boldsymbol{{pls}}\:\boldsymbol{{check}}\:\boldsymbol{{uoto}}\:\boldsymbol{{this}}\:\boldsymbol{{step}}… \\ $$$$=\mid{sinx}+{cosx}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} −\mid{sinx}+{cosx}\mid_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{5}\pi}{\mathrm{4}}} +\mid{sinx}+{cosx}\mid_{\frac{\mathrm{5}\pi}{\mathrm{4}}} ^{\mathrm{2}\pi} \\ $$$$=\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}\right)−\left\{\left(\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)−\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\right\}+\left\{\left(\mathrm{0}+\mathrm{1}\right)−\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\right\} \\ $$$$=\sqrt{\mathrm{2}}\:−\mathrm{1}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}}}+\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}} \\ $$$$=\sqrt{\mathrm{2}}\:+\mathrm{2}\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{2}}\: \\ $$$$=\mathrm{4}\sqrt{\mathrm{2}}\:\:\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{the}}\:\boldsymbol{{answer}} \\ $$
