0-dx-x-x-2-1-3-

Question Number 26769 by julli deswal last updated on 29/Dec/17

$$\underset{\:\mathrm{0}} {\overset{\infty} {\int}}\:\:\frac{{dx}}{\left[{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\right]^{\mathrm{3}} }\:=\: \\ $$

Commented by prakash jain last updated on 29/Dec/17

$${u}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${x}=\mathrm{0},{u}=\mathrm{1};{x}=\infty,{u}=\infty \\ $$$$\Rightarrow\left({u}−{x}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +\mathrm{1} \\ $$$$\Rightarrow{u}^{\mathrm{2}} −\mathrm{2}{ux}=\mathrm{1} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\left({u}−\frac{\mathrm{1}}{{u}}\right) \\ $$$${dx}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\right){du} \\ $$$$\int_{\mathrm{1}} ^{\infty} \frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\right){du}}{{u}^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{u}^{\mathrm{3}} }{du}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{u}^{\mathrm{5}} }{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{\mathrm{2}{u}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{\mathrm{4}{u}^{\mathrm{4}} }\right]_{\mathrm{1}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$

Answered by prakash jain last updated on 29/Dec/17

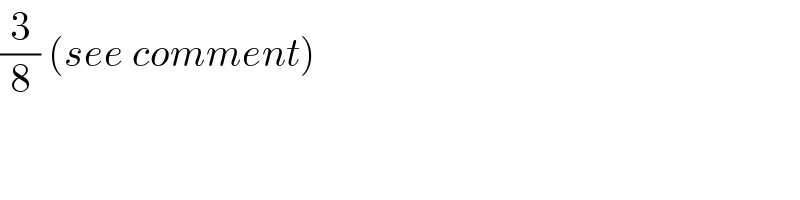
$$\frac{\mathrm{3}}{\mathrm{8}}\:\left({see}\:{comment}\right) \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com