Question Number 53693 by gunawan last updated on 25/Jan/19
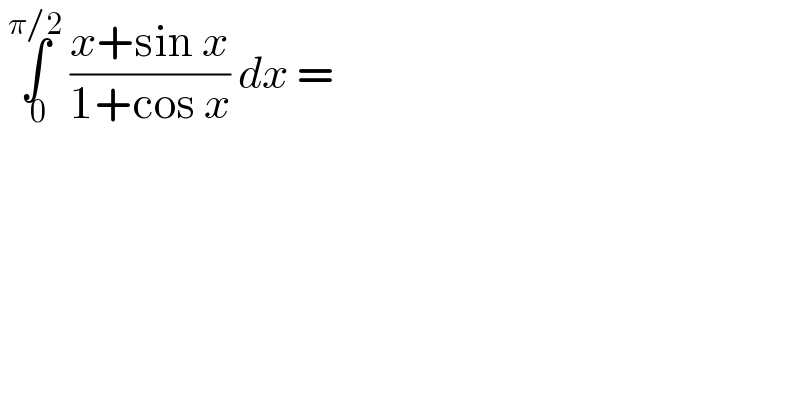
$$\:\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{{x}+\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{cos}\:{x}}\:{dx}\:= \\ $$
Commented by maxmathsup by imad last updated on 25/Jan/19
![let I =∫_0 ^(π/2) ((x+sinx)/(1+cosx)) ⇒I =∫_0 ^(π/2) (x/(1+cosx))dx +∫_0 ^(π/2) ((sinx)/(1+cosx))dx but ∫_0 ^(π/2) ((sinx)/(1+cosx))dx =−∫_0 ^(π/2) (((cosx)^, )/(1+cosx)) dx =−[ln∣1+cosx∣]_0 ^(π/2) =−(−ln(2))=ln(2) ∫_0 ^(π/2) (x/(1+cosx))dx =(1/2) ∫_0 ^(π/2) (x/(cos^2 ((x/2))))dx =(1/2) ∫_0 ^(π/2) x(1+tan^2 ((x/2))dx but ∫_0 ^(π/2) x(1+tan^2 ((x/2)))dx =_((x/2)=t) ∫_0 ^(π/4) (2t)(1+tan^2 t)(2)dt =4 ∫_0 ^(π/4) t(1+tan^2 t)dt by parts u=t and v^′ =1+tan^2 t ⇒ ∫_0 ^(π/4) t(1+tan^2 t)dt =[t tant]_0 ^(π/4) −∫_0 ^(π/4) tant dt =(π/4) + ∫_0 ^(π/4) ((−sint)/(cost)) dt =(π/4) +[ln∣cost∣]_0 ^(π/4) =(π/4) +ln((1/( (√2))))=(π/4) −(1/2)ln(2) ⇒ ∫_0 ^(π/2) x(1+tan^2 ((x/2)))dx =π−2ln(2) ⇒ I =ln(2) +(1/2)(π−2ln(2)) ⇒ I =(π/2) .](https://www.tinkutara.com/question/Q53794.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{x}+{sinx}}{\mathrm{1}+{cosx}}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{x}}{\mathrm{1}+{cosx}}{dx}\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sinx}}{\mathrm{1}+{cosx}}{dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sinx}}{\mathrm{1}+{cosx}}{dx}\:=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\left({cosx}\right)^{,} }{\mathrm{1}+{cosx}}\:{dx}\:=−\left[{ln}\mid\mathrm{1}+{cosx}\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =−\left(−{ln}\left(\mathrm{2}\right)\right)={ln}\left(\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{x}}{\mathrm{1}+{cosx}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{x}}{{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right){dx}\:{but}\right. \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right){dx}\:=_{\frac{{x}}{\mathrm{2}}={t}} \:\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left(\mathrm{2}{t}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)\left(\mathrm{2}\right){dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{t}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt}\:\:\:{by}\:{parts}\:{u}={t}\:{and}\:{v}^{'} =\mathrm{1}+{tan}^{\mathrm{2}} {t}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{t}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt}\:=\left[{t}\:{tant}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{tant}\:{dt} \\ $$$$=\frac{\pi}{\mathrm{4}}\:+\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{−{sint}}{{cost}}\:{dt}\:=\frac{\pi}{\mathrm{4}}\:+\left[{ln}\mid{cost}\mid\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:=\frac{\pi}{\mathrm{4}}\:+{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)=\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right){dx}\:=\pi−\mathrm{2}{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$${I}\:={ln}\left(\mathrm{2}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\pi−\mathrm{2}{ln}\left(\mathrm{2}\right)\right)\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{2}}\:. \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jan/19
![∫_0 ^(π/2) (x/(1+cosx))dx−∫_0 ^(π/2) ((d(1+cosx))/(1+cosx)) ∫_0 ^(π/2) x×(1/(2cos^2 (x/2)))−∫_0 ^(π/2) ((d(1+cosx))/(1+cosx)) now... ∫xsec^2 (x/2)dx x×((tan(x/2))/(1/2))−∫[(dx/dx)∫sec^2 (x/2)dx]dx =2xtan(x/2)−∫((tan(x/2))/(1/2))dx =2xtan(x/2)−2lnsec(x/2) so (1/2)∫_0 ^(π/2) xsec^2 (x/2)−∫_0 ^(π/2) ((d(1+cosx))/(1+cosx)) (1/2)∣2xtan(x/2)−2lnsec(x/2)∣_0 ^(π/2) −∣ln(1+cosx)∣_0 ^(π/2) ={((π/2)tan(π/4)−lnsec(π/4))−(0×tan(0/2)−lnsec0)}−{ln(1+0)−ln(1+1)} ={((π/2)×1−ln(√2) )−(0−0)}−{0−ln2} =(π/2)−(1/2)ln2+ln2 =(π/2)+(1/2)ln2 pls check steps...](https://www.tinkutara.com/question/Q53737.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}}{\mathrm{1}+{cosx}}{dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left(\mathrm{1}+{cosx}\right)}{\mathrm{1}+{cosx}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}×\frac{\mathrm{1}}{\mathrm{2}{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left(\mathrm{1}+{cosx}\right)}{\mathrm{1}+{cosx}} \\ $$$${now}… \\ $$$$\int{xsec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx} \\ $$$${x}×\frac{{tan}\frac{{x}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}}−\int\left[\frac{{dx}}{{dx}}\int{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}\right]{dx} \\ $$$$=\mathrm{2}{xtan}\frac{{x}}{\mathrm{2}}−\int\frac{{tan}\frac{{x}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}}{dx} \\ $$$$=\mathrm{2}{xtan}\frac{{x}}{\mathrm{2}}−\mathrm{2}{lnsec}\frac{{x}}{\mathrm{2}} \\ $$$${so} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {xsec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left(\mathrm{1}+{cosx}\right)}{\mathrm{1}+{cosx}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mid\mathrm{2}{xtan}\frac{{x}}{\mathrm{2}}−\mathrm{2}{lnsec}\frac{{x}}{\mathrm{2}}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\mid{ln}\left(\mathrm{1}+{cosx}\right)\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\left\{\left(\frac{\pi}{\mathrm{2}}{tan}\frac{\pi}{\mathrm{4}}−{lnsec}\frac{\pi}{\mathrm{4}}\right)−\left(\mathrm{0}×{tan}\frac{\mathrm{0}}{\mathrm{2}}−{lnsec}\mathrm{0}\right)\right\}−\left\{{ln}\left(\mathrm{1}+\mathrm{0}\right)−{ln}\left(\mathrm{1}+\mathrm{1}\right)\right\} \\ $$$$=\left\{\left(\frac{\pi}{\mathrm{2}}×\mathrm{1}−{ln}\sqrt{\mathrm{2}}\:\right)−\left(\mathrm{0}−\mathrm{0}\right)\right\}−\left\{\mathrm{0}−{ln}\mathrm{2}\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}+{ln}\mathrm{2} \\ $$$$=\frac{\pi}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2} \\ $$$${pls}\:{check}\:{steps}… \\ $$$$ \\ $$
